Introduction
Un champ tournant est un champ magnétique dont l’orientation pivote au cours du temps.
Les champs tournants sont créés afin qu’ils entraînent des pièces présentant une certaine polarité créant ainsi des moteurs.
Si le champ tournant est créé par des pièces fixes (que l’on appellera stator) alimentées en alternatif, il entraine (c’est donc un moteur) un rotor (si c’est à la même vitesse que le champ tournant c’est alors un moteur synchrone sinon c’est un moteur asynchrone) qui aura tendance à aligner son champ magnétique (champ magnétique créé par un aimant permanent ou un bobinage alimenté en continu pour le moteur synchrone ou champ magnétique induit par le fait que le rotor voit le champ tournant varier autour de lui, c’est donc un moteur asynchrone) sur celui du champ tournant créé par le stator.
Pour créer un champ tournant deux possibilités :
- Rotation d'un aimant ou d’un électroaimant (alimenté en continu): c'est en général le cas de l'alternateur
- Bobinages fixes espacés de 120° et parcourus par des courants triphasés: c'est le cas du moteur synchrone ou asynchrone
Production d'un champ tournant
Champ créé par une bobine du stator
La création d'un champ magnétique est réalisé par le passage du courant dans une bobine:
| La bobine parcourue par un courant devient un électroaimant et attire une boussole | 
|
| Influence de l'intensité de courant sur le champ magnétique | 
|
| Courant sinusoïdal dans une bobine | 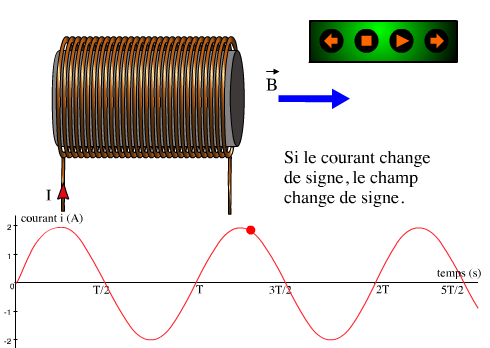
|
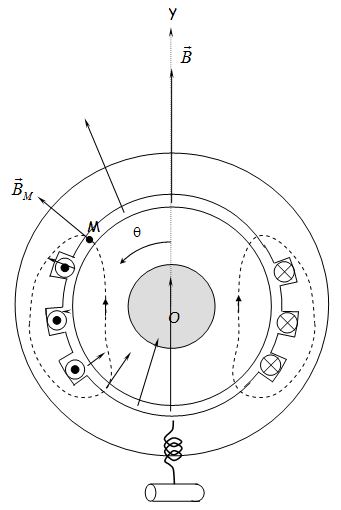
Si on regarde la création du champ au niveau du stator, on peut écrire l'expression du champ magnétique dans l'entrefer du stator.
Le champ magnétique en un point M dépend :
- de la position du point M dans l'entrefer,
- du temps puisque le courant est de la forme \( i = cos \omega t \)
D'où l'expression : \( B\left( {M,t} \right) = B_0 \cos \left( {\omega t} \right) \cdot \cos \left( \theta \right) \)
Où B est orienté perpendiculairement à l’entrefer.
Somme de champs créés par plusieurs bobines du stator
Si la machine est bipolaire
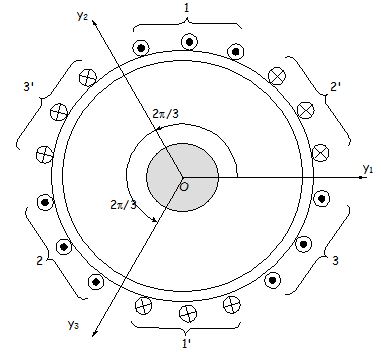
On considère trois enroulements formés de trois bobines identiques, chacune alimentée par une tension issue du réseau triphasé dont les axes des bobines sont décalés de 120° .
Chaque tension n'alimente qu'une bobine et ne crée donc que deux pôles (un pôle Nord et un pôle Sud sur chaque bobine).
Elles sont respectivement parcourues par les courants:
\( \eqalign{ & i_1 (t) = \hat I\cos \omega t \cr & i_2 (t) = \hat I\cos \left( {\omega t - \frac{{2\pi }}{3}} \right) \cr & i_3 (t) = \hat I\cos \left( {\omega t - \frac{{2\pi }}{3}} \right) \cr} \)
Ces courants génèrent des champs magnétiques qui s'additionnent.
| Somme vectorielle de deux champs magnétiques décalés de 120° | 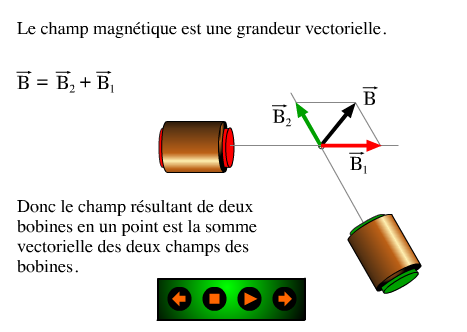
|
| Somme des champs des trois bobines décalées de 120° alimentées par du triphasé | 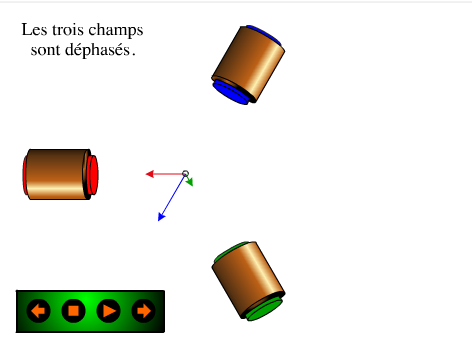
|
Remarque : l’axe de \( \vec B \) coïncide avec l’axe d’une phase, chaque fois que l’intensité du courant est maximale dans cette phase donc l’ordre des phases impose le sens de rotation de \( \vec B \), donc le sens de rotation de la machine.

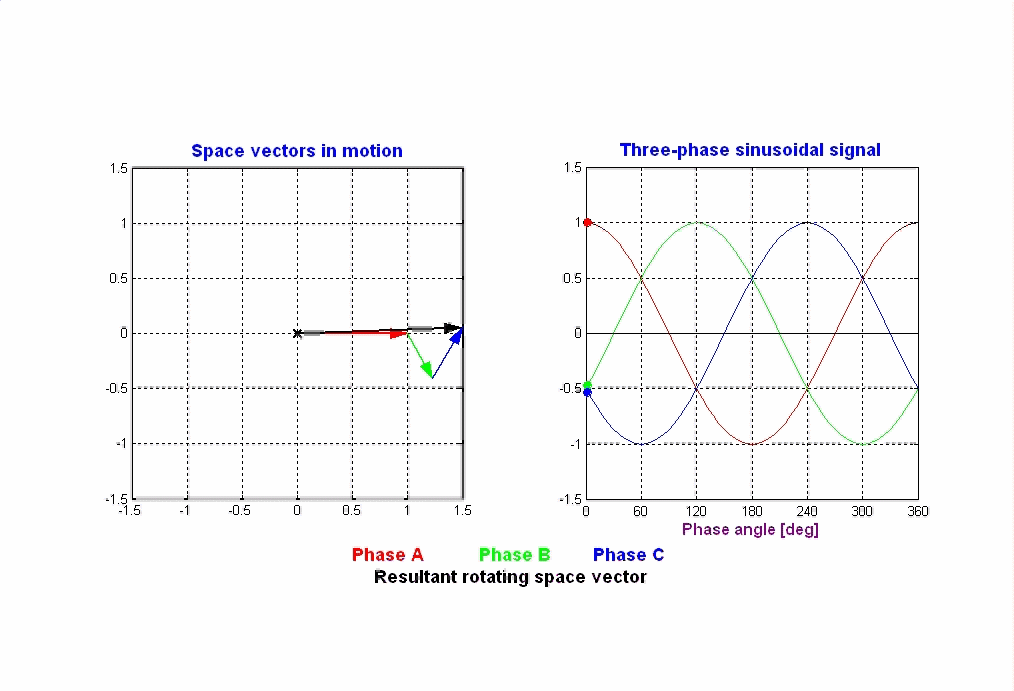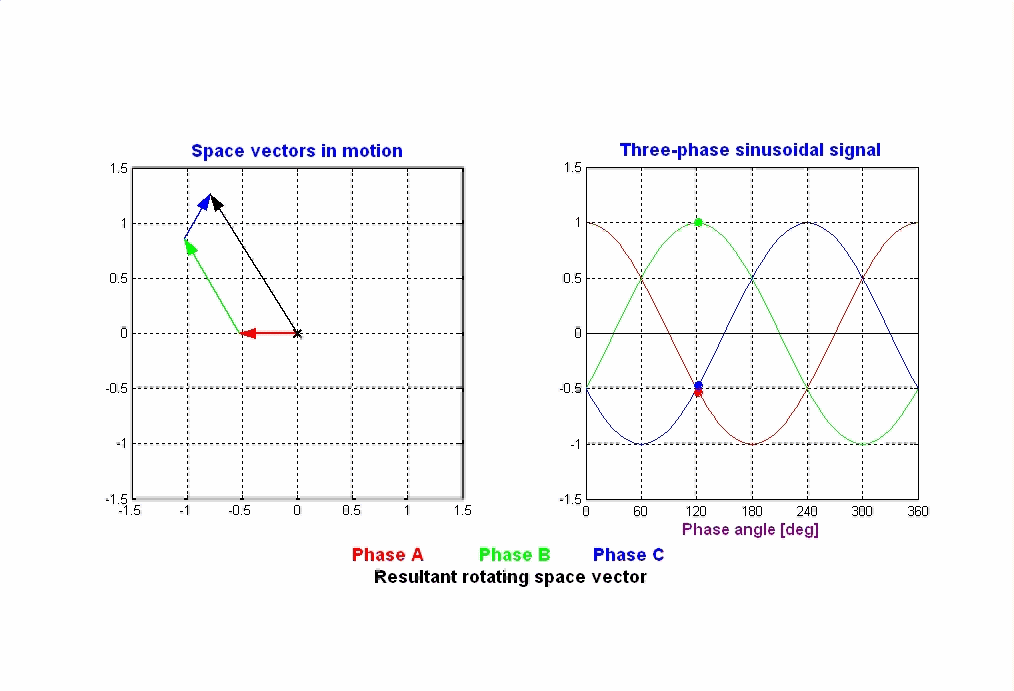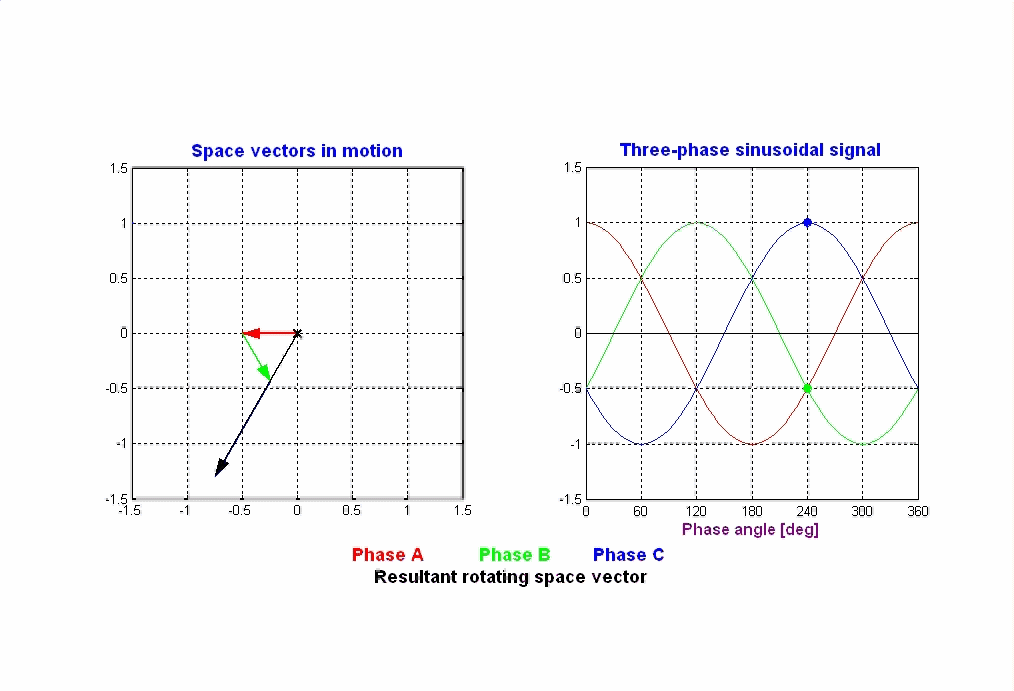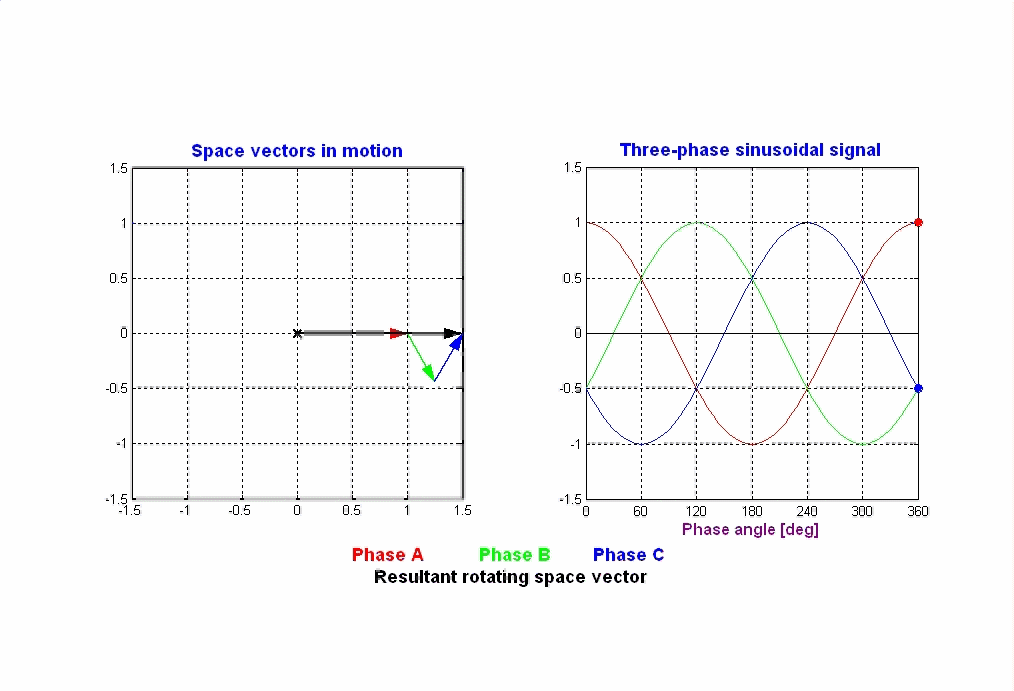
Généralisation à une machine multipôlaire
Chaque enroulement comporte p bobines en série ( p paires de pôles ) disposées de manière à faire apparaitre une succession de pôles N et S:
- chaque phase alimente p bobines en série;
- le décalage entre les axes de 2 bobines successives est \( \frac{1}{3}\left( {\frac{{2\pi }}{p}} \right) \)
Par comparaison avec une machine bipôlaire, l’axe du champ magnétique tournant \( \vec B \) coïncide avec l’axe d’une bobine chaque fois que l’intensité est maximale dans la phase alimentant cette bobine. L’angle entre les axes de 2 bobines successives étant p fois plus petit, la fréquence f est p fois plus grande
| \( f = p n \) |
Principe de la machine synchrone
Principe de la machine asynchrone
Composants mécaniques du moteur tri Attach:les composants mecaniques du moteur tri.swf
Aperçu global en Flash
Aperçu des notions sur le champ tournant:









