| \( P_{rel} = {P_{abs}} - {P_{atm}} \) |
| \( \Delta p = {\rm{ }}\rho {\rm{ }}g{\rm{ }}\Delta z\ \) |
et principe de conservation du débit
- Expression de Bernoulli
- Si la conduite ne présente pas de pertes ou gains
| \( \frac{1}{2}\rho {\rm{ }}\left( {v_2^2 - v_1^2} \right) + \rho g{\rm{ }}({z_2} - {z_1}) + \left( {{p_2} - {p_1}} \right) = 0\ \) |
- Si la conduite présente des pertes ou gains
| \( \underbrace {\rho \frac{{v_1^2}}{2} + \rho g{z_1} + {p_1}}_{{\rm{énergies}}\,\,\,{\rm{volumiques}}\,\,{\rm{en}}\,\,{\rm{1}}} + \frac{{{P_f} + {P_T} + {P_P}}}{{{q_V}}}\, = \underbrace {\rho \frac{{v_2^2}}{2} + \rho g{z_2} + {p_2}}_{{\rm{énergies}}\,\,\,{\rm{volumiques}}\,\,{\rm{en}}\,\,{\rm{2}}} \) |
- \( P < 0 \) si l’énergie est reçue par le fluide (ex. : turbine \( P_T \) ) ou pertes singulières ou régulières \( P_f \));
- \( P > 0 \) si l’énergie est fournie par le fluide (ex. : pompe \( P_P \).
- L'expression de la hauteur manométrique d'une pompe de puissance P est donnée par
| \( H = \frac{P}{{\rho gQ}}\ \) |
- Savoir lire les courbes d'une pompe
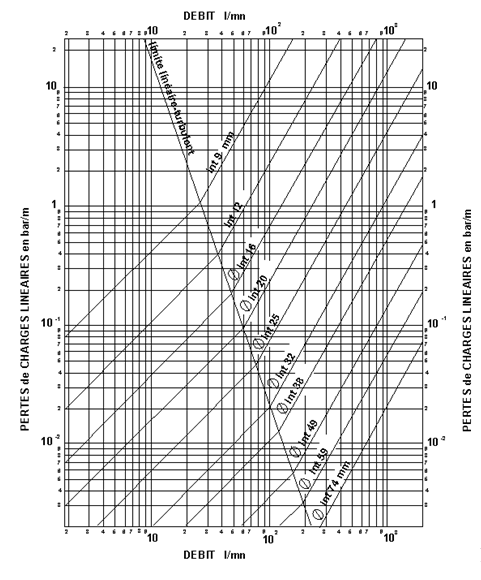
- Savoir lire sur une abaque de pertes de charges
- Exemple
- un tuyau de diamètre intérieur 9 mm de 5m de long parcouru par un débit de 0.7 l/min, générera des pertes linéaires de 0,3 bar/m, soit 0.3x5 = 1,5 bar