Millman en continu
Si l’on cherche la tension dans un nœud d’un montage connaissant les tensions « avoisinantes » , le méthode de Millman peut être rapide et efficace mais souffre parfois d’une certaine lourdeur et n’est donc à employer que pour des cas où les classiques lois nœuds, lois des mailles s’avèrent fastidieuses.
La méthode de Millman démontre que la tension en un point d'un circuit est donnée par
| \( {V_A} = \frac{{\sum\limits_{k = 1}^n {\frac{{{V_k}}}{{{R_k}}}} }}{{\sum\limits_{k = 1}^n {\frac{1}{{{R_k}}}} }} \) |
Exemple:
| \( {V_A} = \frac{{\frac{{{V_1}}}{{{R_1}}} + \frac{{{V_2}}}{{{R_2}}} + \frac{{{V_3}}}{{{R_3}}}}}{{\frac{1}{{{R_0}}} + \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}} + \frac{1}{{{R_3}}}}} \) | 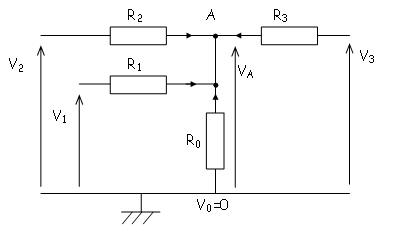
|
le théorème de Millman n’est qu’un cas particulier de la loi des nœuds :
Dans le montage ci-dessus la somme des courants est nulle : \( {I_{{R_0}}} + {I_{{R_1}}} + {I_{{R_2}}} + {I_{{R_3}}} = 0 \)
Chaque courant est tel que : \( {I_{{R_i}}} = \frac{{{V_i} - {V_A}}}{{{R_i}}} \)
Donc : \( \frac{{{V_0} - {V_A}}}{{{R_0}}} + \frac{{{V_1} - {V_A}}}{{{R_1}}} + \frac{{{V_2} - {V_A}}}{{{R_2}}} + \frac{{{V_3} - {V_A}}}{{{R_3}}} = 0 \)
Si on rassemble d’un coté les termes en \( V_A \) : \( \underbrace {\frac{{{V_0}}}{{{R_0}}}}_0 + \frac{{{V_1}}}{{{R_1}}} + \frac{{{V_2}}}{{{R_2}}} + \frac{{{V_3}}}{{{R_3}}} = \frac{{{V_A}}}{{{R_0}}} + \frac{{{V_A}}}{{{R_1}}} + \frac{{{V_A}}}{{{R_2}}} + \frac{{{V_A}}}{{{R_3}}} \)
Donc \( \frac{{{V_1}}}{{{R_1}}} + \frac{{{V_2}}}{{{R_2}}} + \frac{{{V_3}}}{{{R_3}}} = {V_A}\left( {\frac{1}{{{R_0}}} + \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}} + \frac{1}{{{R_3}}}} \right) \) soit \( {V_A} = \frac{{\frac{{{V_1}}}{{{R_1}}} + \frac{{{V_2}}}{{{R_2}}} + \frac{{{V_3}}}{{{R_3}}}}}{{\frac{1}{{{R_0}}} + \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}} + \frac{1}{{{R_3}}}}} \) l’expression trouvée précédemment
Millman en complexe
Le théorème de Millman est tout autant applicable avec des impédances complexes:
| \( {\underline{V}_A} = \frac{{\sum\limits_{k = 1}^n {\frac{{{\underline{V}_k}}}{{{\underline{Z}_k}}}} }}{{\sum\limits_{k = 1}^n {\frac{1}{{{\underline{Z}_k}}}} }} \) |
Le théorème de Millman n'est en fait qu'une conséquence de la loi des nœuds et de la loi d'Ohm et peut être aisément retrouvé
Démo Vidéo
| E-Learning Physique: Electrocinétique : Le théorème de Millman, utilité-difficultés- signification (23'48") |
| https://youtu.be/TL_98zHyXOM |





