Il est nécessaire d’introduire une nouvelle puissance que l’on appellera puissance déformante afin de rétablir une égalité entre les puissances apparente, active, réactive et déformante.
On appelle D la puissance dite "déformante". Cette puissance est liée à la présence d’harmoniques dans le courant ou la tension, c'est à dire au fait que l'un ou l'autre est non sinusoïdal.
Si, seul le courant n’est pas sinusoïdal :
| \(D = V \times \sqrt {\sum\limits_{n = 2}^\infty {I_n^2} } = V \times \sqrt {{I^2} - I_1^2} = V \times {I_1} \times THD\) |
En effet partant de la définition de la puissance apparente S
\({S^2} = {V^2}{I^2} = {V^2}\left( {I_1^2 + I_2^2 + I_3^2 + I_4^2 + ...} \right)\)
On peut extraire le terme à la fréquence fondamentale
\({S^2} = {V^2}I_1^2 + {V^2}\left( {I_2^2 + I_3^2 + I_4^2 + ...} \right)\)
Puis décomposer \( I_1 \) en sa composante active et réactive
\({S^2} = {V^2}\left( {I_a^2 + I_r^2} \right) + {V^2}\left( {I_2^2 + I_3^2 + I_4^2 + ...} \right)\)
Ce qui fait apparaitre la puissance active, la puissance réactive, et un nouveau terme que l’on nommera puissance déformante.
\({S^2} = \underbrace {{V^2}I_1^2\cos {\varphi _1}}_{{P^2}} + \underbrace {{V^2}I_1^2\sin {\varphi _1}}_{{Q^2}} + \underbrace {{V^2}\left( {I_2^2 + I_3^2 + I_4^2 + ...} \right)}_{{D^2}}\)
Rappel: Les diverses puissances sont donc liées par la relation :
| \({S^2} = {P^2} + {Q^2} + {D^2}\) |
On peut donc donner une représentation à trois dimensions de la participation de la puissance déformante dans la puissance apparente :
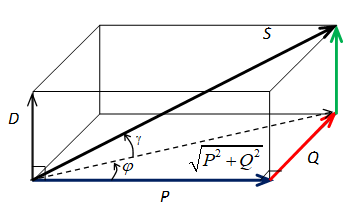
Si les courants et les tensions sont sinusoïdaux, alors \( D=0 \).
Et dans ce cas on retrouve les relations plus classiques \({S^2} = {P^2} + {Q^2} \)





