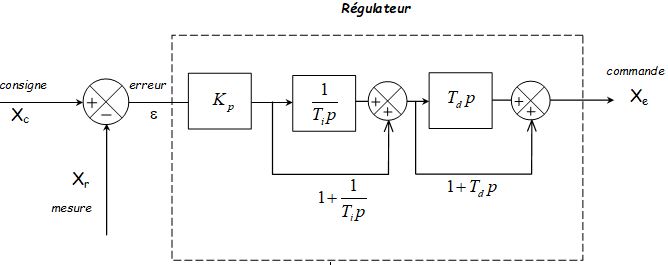
Structure série
\( {X_e} = {K_p}\left[ {\varepsilon \left( {1 + \frac{{{T_d}}}{{{T_i}}}} \right) + \frac{1}{{{T_i}}}\int\limits_0^t {\varepsilon (t)dt} + {T_d}\frac{{d\varepsilon (t)}}{{dt}}} \right] + \frac{{{K_p}}}{{{T_i}}}\int\limits_{ - \infty }^0 {\varepsilon (t)dt} \)
\( C(p) = \frac{{{X_e}(p)}}{{\varepsilon (p)}} = {K_p}\left( {1 + \frac{1}{{{T_i}p}}} \right)\left( {1 + {T_d}p} \right) \)
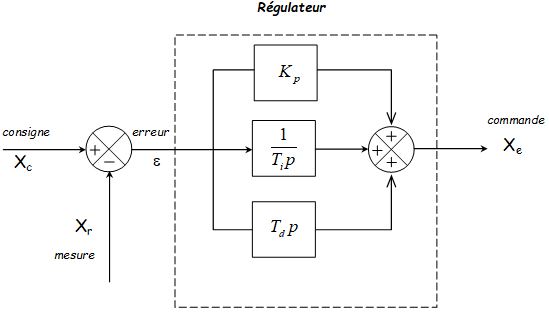
Structure parallèle
\( {X_e} = {K_p}\varepsilon + \frac{1}{{{T_i}}}\int\limits_0^t {\varepsilon (t)dt} + {T_d}\frac{{d\varepsilon (t)}}{{dt}} + \frac{1}{{{T_i}}}\int\limits_{ - \infty }^0 {\varepsilon (t)dt} \)
\(C(p) = \frac{{{X_e}(p)}}{{\varepsilon (p)}} = {K_p} + {T_d}p + \frac{1}{{{T_i}p}} \)
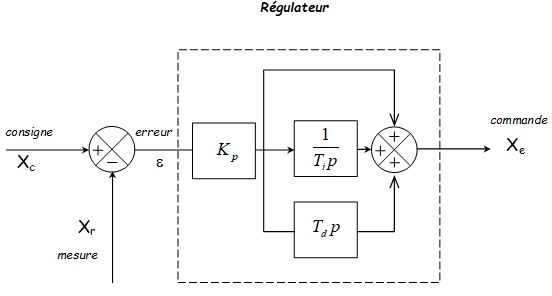
Structure mixte
\( {X_e} = {K_p}\left[ {\varepsilon + \frac{1}{{{T_i}}}\int\limits_0^t {\varepsilon (t)dt} + {T_d}\frac{{d\varepsilon (t)}}{{dt}}} \right] + \frac{{{K_p}}}{{{T_i}}}\int\limits_{ - \infty }^0 {\varepsilon (t)dt} \)
\( C(p) = \frac{{{X_e}(p)}}{{\varepsilon (p)}} = {K_p}\left[ {1 + {T_d}p + \frac{1}{{{T_i}p}}} \right] \)