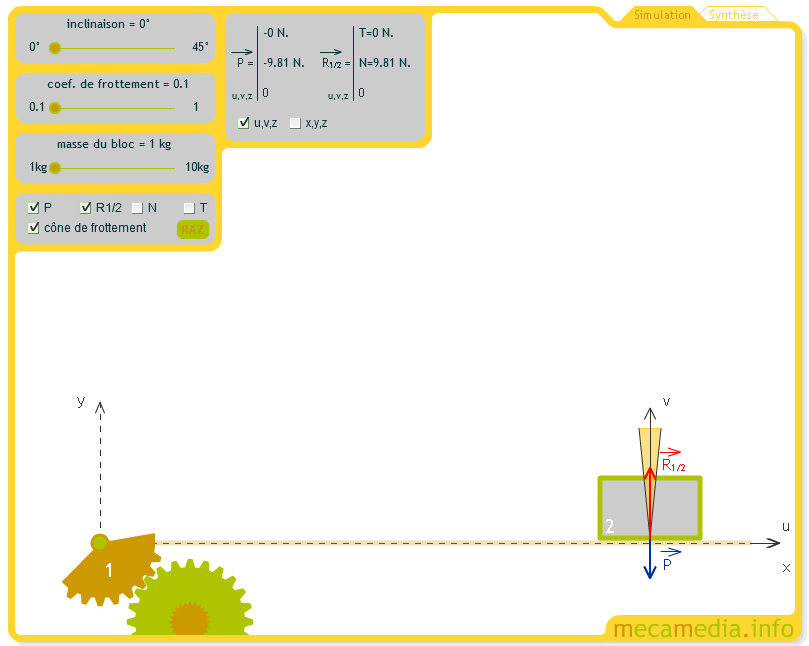
Les forces de frottement des solides:
Définition
- Si deux surfaces en contact se déplacent ou glissent l’une par rapport à l’autre, on dit qu’il y a frottement.
- Quand ces surfaces tendent à glisser mais ne se déplacent pas, on parle d’adhérence.
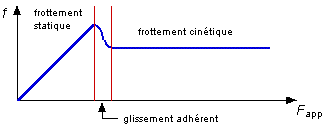
Quand la force devient supérieure à \( {F_{\lim }} = {\mu _S}.R \) , le colis glisse sur le sol. Ce mouvement continuera à vitesse uniforme si on applique \( F’=\mu \cdot R ( <{\mu _S}.R \), c’est à dire <Flim).
Il faut F>Flim pour mettre l’objet en mouvement mais une force inférieure sera suffisante pour maintenir le mouvement. La force \( \vec f \) s’opposant au mouvement est telle que \( f = \mu.R \) avec \(\mu\) coefficient de frottement dynamique.
Exemples : (donnés à titre indicatifs, de grosses variations peuvent apparaitre)
- Pneu de voiture sur route :\( {\mu _S}=0,8 \) ; \( \mu=0.6 \) ; \( \mu=0.1 à 0.3 \) sur sol mouillé.
- Acier sur acier : \( {\mu _S}=0,18 \) ; lubrifié: \( {\mu _S}=0,12 \) ; \( \mu=0.15 \) ; lubrifié : \( \mu=0.09 \)
Le coefficient de frottement dépend essentiellement de la nature des matériaux en contact et de la qualité des surfaces en contact. Il est indépendant des efforts exercés ainsi que de l’étendue des surfaces en contact.
Dans les cas abordés, la différence entre force d'adhérence et de frottement seront négligées et considérées comme égales
Si on exerce une poussée latérale \( \vec F \) passant par le centre de gravité G, deux cas sont possibles :
- Il n’y a pas de mouvement, le colis est en équilibre. Il existe (d’après le principe fondamental de la dynamique) une force d’adhérence \( {\vec f} \) égale à \( \vec F \) et de sens opposé.\( {\vec f} \) s’oppose au déplacement éventuel de l’objet vers la droite (dans ce cas). Si la force \( \vec F \) augmente la force de frottement va augmenter elle aussi. La résultante des forces de réactions \( \vec f + \vec R\) présente un angle \( %alpha_1 \) avec la verticale qui augmente lui aussi avec la force. Lorsque la force \( {\vec F} \) augmente la force de frottement \( {\vec f} \) augmente aussi et l'angle \( %alpha \) aussi jusqu'à un angle limite \( %alpha_lim \)
- Si \( \vec F \) devient suffisante, \( \vec F > \vec F_{\lim } \) , l’objet se met à glisser dans le même sens que \( \vec F \). La résultante \( \vec f + \vec R\) présente le même angle \( %alpha_lim \) trouvé au moment de l'amorce du glissement. Le vecteur \( \vec f \) reste alors constant, si la force de traction \( \vec F \) reste constante et supérieure à la force de frottement, le solide se déplace alors à accélération constante déterminée par le principe fondamental de la dynamique.
Relation
La valeur de cet angle limite permet de déterminer la force de frottement.
De part la construction graphique, la force de frottement est donnée par \( f = tan (\alpha_{\lim }) . R \)
| \( f = {\mu _S}.R = tan (\alpha_{\lim }) . R \) |
On note coefficient de frottement statique ou coefficient d’adhérence \( {\mu _S} = \frac{{{F_{\lim }}}}{R} = \frac{{{f_{a\lim }}}}{R} \).

Où \( {\mu _S} = \tan {\alpha _{\lim }} \) avec \( \alpha _{\lim } \) angle de frottement statique.
Animations :
Les forces de frottement d'un solide dans un fluide:
Expression de la trainée:
La force de frottement d'un objet sur un fluide est aussi appelée trainée.
Elle dépend
- de la masse volumique \( \rho \) du fluide dans lequel le solide se déplace en \( kg/m^3 \)
- de la vitesse du solide \( v \) en \( m/s \)
- de la surface faisant face au déplacement \( S \) en \( m^2 \)
- d'un coefficient de forme traduisant le pouvoir de pénétration du solide appelé coefficient de trainée\( C_x \)
La force de frottement prend donc l'expression:
| \( R = \frac{1}{2} C_x \rho S v^2\) |
Vitesse atteinte par un objet en chute libre:
La RFD appliquée à un objet en chute libre s'écrit ainsi:
\( m \cdot a = m \cdot g - \frac{1}{2} C_x \rho S v^2\)
soit \( m \cdot \frac{dv}{dt} = m \cdot g - \frac{1}{2} C_x \rho S v^2\)
cette équation différentielle est telle que \( V_{max} = \sqrt{\frac{2 m g}{C_x \rho g}} \)
L'équation différentielle du type \( \frac{dy}{dt}=1-y^2 \) a pour solution \( y=tanh(t) \)
donc la solution de cette équation est \( v(t) = V_{max} tanh\frac{t}{T} \)