Indice horaire h:
Sur un transformateur monophasé les tensions qui pointent sur les bornes homologues (marquées d’un point) sont en phase.
Alors que sur un transformateur monophasé le primaire et le secondaire sont en phase (ou en opposition de phase), sur un transformateur triphasé le primaire et le secondaire seront déphasés d’un angle qui dépendra des couplages choisis au primaire et au secondaire.
L’indice horaire permet de connaître le déphasage qu’il existe entre le primaire et le secondaire d’un transformateur, celui -ci étant couplé au primaire et au secondaire (en triangle, en étoile ou en zigzag.).
Un transformateur triphasé peut être vu comme composé de 3 transformateurs monophasés.
On peut alors parler de la colonne A qui supporte les tensions primaire VA et secondaire Va puis la colonne B puis la colonne C. Ces 3 colonnes forment donc notre transformateur triphasé.
Comme pour le transformateur monophasé, chaque colonne du transformateur triphasé présente des tensions qui si elles pointent sur les bornes homologues seront en phase. Donc \( V_A \) en phase avec \( V_a \) , \( V_B \) avec \( V_b \), \( V_C\) avec \( V_c \)
Les couplages effectués au primaires et secondaires sont résumés par un ensemble de deux lettres
- La première lettre désigne le couplage Haute Tension et sera notée en majuscule (Y : étoile, D : triangle , Z : zig-zag)
- La deuxième lettre désigne le couplage Basse Tension et sera notée en minuscule (y : étoile, d : triangle , z : zig-zag)
- L’éventuelle lettre n : indique la présence du neutre
Le couplage étoile permet la sortie du neutre ce qui très utile en basse tension, et par conséquent mettre à disposition un réseau de tensions simple et un réseau de tensions composées, mais également il est utile pour évacuer le courant de neutre dans le cas d’une charge déséquilibrée.
Le couplage triangle ne permettant que la distribution d’une tension verra son emploi limité à la distribution/transport de l’énergie électrique.
Dans le cas du couplage zig-zag, le secondaire du transformateur est découpé en 2 enroulements. Il permet de limiter l’influence des déséquilibres de courants.
Les diverses possibilités de couplage entre le primaire et le secondaire va amener des déphasages différents entre le primaire et le secondaire.

L’indice horaire est un nombre h multiplié par \(\frac{\pi }{6}\) (ou 30° ) qui indique:
- le déphasage \( \psi \) compté en sens horaire
- d’une tension simple \(\overrightarrow {{V_{an}}} \) ou composée \(\overrightarrow {{U_{ab}}} \) du secondaire par rapport à une tension simple ou composée du primaire \(\overrightarrow {{V_{AN}}} \) ou \(\overrightarrow {{U_{AB}}} \).
On peut donc placer la tension \(\overrightarrow {{U_{AB}}} \) du primaire au niveau de midi et regarder où se place la tension secondaire.
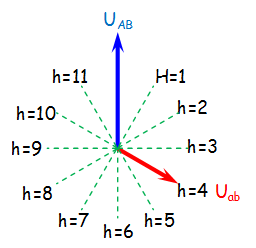
le rapport de transformation qui est défini par le rapport de la tension du secondaire sur le primaire n’est plus égal à N2/N1 mais dépendra du couplage choisi au primaire et au secondaire.
Choix des couplages :
- La présence du neutre dans les installations basse tension permet d’obtenir 2 types de tension : simple pour les usages domestiques usuels ou composée pour l’alimentation des petits moteurs.
- Il est intéressant en haute tension d’avoir un couplage qui fait apparaître le neutre. Le neutre, les parties métalliques et magnétiques sont mises au potentiel de la terre ce qui réduit l’isolement des bobines haute tension.
- On évite d’avoir le même couplage au primaire et au secondaire pour ne pas transmettre intégralement le déséquilibre éventuel des courants. Si le neutre est nécessaire des deux côtés alors le montage Yz ou Zy est alors communément employé.
Couplages courants :

Exemple :
Couplage étoile triangle Yd1 :

- Les tensions sur une même colonne \({\vec V_A}\) et \({\vec V_a}\) sont toujours en phase : on recherche le déphasage de \({\vec V_{AN}}\) par rapport à \({\vec V_{an}}\)(identique à \({\vec U_{AB}}\) par rapport à \({\vec U_{ab}}\) ). La construction de Fresnel donne \({\vec U_{AB}}=\vec V_A - \vec V_B\) et \({\vec V_{a}}=\vec U_{ab}\) nous permet de déterminer \( \psi_{\frac{U_{ab}}{U_{AB}}}=\frac{\pi}{6} \) donc l’indice horaire est de 1
- Rapport des tensions \(\frac{{{V_{an}}}}{{{V_{AN}}}}\) ou \(\frac{{{U_{ab}}}}{{{U_{AB}}}}\): comme \(\frac{{{U_{ab}}}}{{{V_{AN}}}} = \frac{{{N_2}}}{{{N_1}}}\) or \( {U_{ab}} = \sqrt 3 \cdot {V_{an}} \) donc \(\frac{{{V_{an}}}}{{{V_{AN}}}} = \frac{{{N_2}}}{{\sqrt 3 {N_1}}}\)
Couplage zig zag Yz 11:
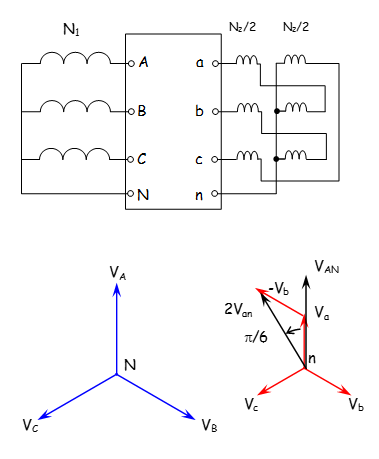
- Les tensions sur une même colonne \({\vec V_A}\) et \({\vec V_a}\) sont toujours en phase : on recherche le déphasage de \({\vec U_{ab}}\) par rapport à \({\vec U_{ab}}\) (identique à \({\vec V_{an}}\) par rapport à \({\vec V_{AN}}\) ). La construction de Fresnel donne \( \vec V_{A}=\vec V_{AN} \) et \( \vec V_{an} =\frac{\vec V_a}{2}-\frac{\vec V_b}{2} \) nous permet de déterminer \( \psi_{\frac{V_{an}}{V_{AN}}}=11 \times \frac{\pi}{6} \) donc l’indice horaire est de 11.
- Rapport des tensions \(\frac{{{V_{an}}}}{{{V_{AN}}}}\) ou \(\frac{{{U_{ab}}}}{{{U_{AB}}}}\):
comme \(\frac{{{V_a}}}{{{V_{AN}}}} = \frac{{{N_2}}}{{{N_1}}}\) et \({\vec V_{an}} = \frac{{{{\vec V}_a}}}{2} - \frac{{{{\vec V}_b}}}{2}\) fait apparaître un triangle isocèle dans lequel \(2{V_{an}} = \sqrt 3 \times {V_a}\) donc \( \frac{2}{{\sqrt 3 }} \times {V_{an}} = {V_a} \) donc \( \frac{{\frac{2}{{\sqrt 3 }} \times {V_{an}}}}{{{V_{AN}}}} = \frac{{{N_2}}}{{{N_1}}} \) soit \( \frac{{{V_{an}}}}{{{V_{AN}}}} = \frac{{{N_2}}}{{{N_1} \times \frac{2}{{\sqrt 3 }}}} = \frac{{\sqrt 3 }}{2} \cdot \frac{{{N_2}}}{{{N_1}}} \) donc \(\frac{{{V_{an}}}}{{{V_{AN}}}} = \frac{{\sqrt 3 }}{2}\frac{{{N_2}}}{{{N_1}}}\)
Fichier Flash relatif aux indices horaires:
Vidéo
Chapitre 4.2 Transformateur - Les indices horaires des transformateurs en triphasé Ismail SADKY (3'18") https://youtu.be/POhCQE2BS8I







