Essai à vide sous tension nominale:
Comme en monophasé l'essai à vide sous tension nominale va permettre de déterminer
- le rapport de transformation \( m=\frac{U_{ab}}{U_{AB}} \)
- la résistance modélisant les pertes fer \( R_f \).
En effet, à vide, le courant est faible donc les pertes Joules (proportionnelle à \( I^2 \)) sont négligeables.
Les pertes fer \( {P_{fer}} = {P_{10}} - \underbrace {{P_{j10}}}_{3{r_1}I_{10}^2} \) et donc \( {R_{fer} } \) car \( {P_{fer}}\mathop \approx \limits_{Kapp} \frac{{3V_1^2}}{{{R_{fer} }}} = \frac{{U_1^2}}{{{R_{fer} }}} \).
De même la puissance réactive peut-être déterminée par \( {Q_{10}} = \sqrt {{S_{10}}^2 - P_{10}^2} = \sqrt {{{\left( {\sqrt 3 {U_1}{I_{10}}} \right)}^2} - P_{10}^2} \)
Les éléments qui consomment de la puissance réactive dans la modélisation sont tels que \( {Q_{10}} = 3{\ell _{f1}}\omega I_{10}^2 + \frac{{3V \prime _1^2}}{{{L_\mu }\omega }}\)
\( {Q_{10}} = \mathop \approx \limits_{Kapp} \frac{{3V_1^2}}{{{L_\mu }\omega }} = \frac{{U_1^2}}{{{L_\mu }\omega }} \)
soit donc \( {Q_{10}} = \frac{{3V_1^2}}{{{L_\mu }\omega }} = \frac{{U_1^2}}{{{L_\mu }\omega }} \) et ainsi \( L_m \)
Essai en court circuit à courant nominal sous tension réduite
Les pertes Joules lors d'un essai en court-circuit sous tension réduite permettent de déterminer la résistance modélisant les pertes joules ramenées au secondaire : \( R_s \)
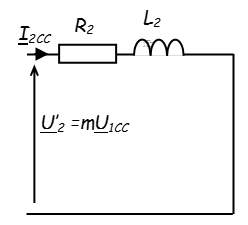
| \({R_S} = \frac{{{P_{1CC}}}}{{3 \times I_{2CC}^2}}\) |
On en déduit aisément \({Z_2} = \frac{{m{V_{1CC}}}}{{{I_{2CC}}}} = \sqrt {R_2^2 + \left( {{L_2}\omega } \right)_2^2} \)
donc \({X_S} = {L_S}\omega = \sqrt {{{\left( {\frac{{m{V_{1CC}}}}{{{I_{2CC}}}}} \right)}^2} - R_S^2} = \frac{{{Q_{1CC}}}}{{3I_{2CC}^2}}\)






