Vidéo
| Les Inducteurs Expliqués 10’19’’ Mentalité Ingénieur |
| https://youtu.be/16TAJREID_0 |
Description

La bobine, aussi appelée inductance, ou self-inductance, est un conducteur enroulé sur lui même.
- il comporte un nombre N d'enroulement aussi appelés spires
- cette bobine présente une longueur \( l \) sur laquelle est enroulé le fil de cuivre
- le rapport \( \frac{N}{l} \) traduit donc la densité de l'enroulement
- cette bobine peut enserrer un matériaux ferromagnétique de perméabilité magnétique \( \mu \) afin de canaliser les lignes de champ magnétique.

De gauche à droite : une bobine rectiligne, une bobine circulaire et une bobine moulée.
Symboles
| Symbole générique de la bobine |  |
| bobine à noyaux de ferrite | 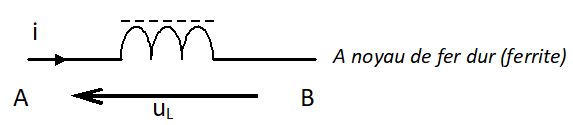 |
| bobine à noyaux de fer doux | 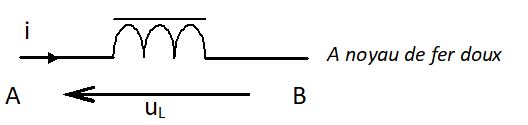 |
| bobine ajustable | 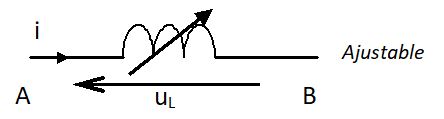 |
Que se passe-t-il dans une bobine?
Dans une bobine, le champ magnétique qui apparait lors de la croissance du courant la traversant génère un champ magnétique croissant. La bobine s'oppose à cette variation de champ magnétique et limite la montée du courant et ce d'autant plus que le nombre de spire et donc le champ magnétique est important. C'est pourquoi les matériaux ferreux insérés dans les bobines canalisant le champ magnétique et l'augmentant, augmentent par là même, la caractéristique de la bobine.
Association de bobines
Bobines en série:

La bobine équivalente à des bobines en séries s'ajoutent :en effet les champs magnétiques s'ajoutent.
| \( L_{eq}=L_1+L_2 \). |
Bobines en parallèles :

L'inverse de l'inductance équivalente à des bobines en parallèles est la somme des inverses de chacune des inductances.
\( \frac{1}{L_{eq}}=\frac{1}{L_1}+\frac{1}{L_2} \).
Relation entre U et I, cas général
Quelque soit la forme de la tension ou du courant dans une bobine, la tension et le courant sont liés par la relation
| \( u = L \frac{di}{dt} \) |
La tension est donc le produit de la valeur de la bobine par la dérivée ou pente du courant.
- si le courant est une sinusoïde, alors la tension sera un cosinus (soit une sinusoïde déphasée de \( \frac{\pi}{2} \)
- si le courant est en dents de scie, alors la tension est en créneaux
- si le courant est en créneaux alors des pics brutaux apparaissent sur la tension au moment de chaque transition
- si le courant est continu, la dérivée étant nulle, alors la tension sera nulle, la bobine se comporte comme un court-circuit.
Tension moyenne dans une bobine soumise à un courant périodique
La tension moyenne dans une bobine soumise à un courant périodique est nulle
| Si i(t) périodique \( \left\langle u \right\rangle = \left\langle L \frac{di}{dt} \right\rangle = 0 \) |
Si le courant est périodique : \( i\left( t \right) = i\left( {t + T} \right) \)
- donc \( \left\langle {{u_L}\left( t \right)} \right\rangle = \int\limits_t^{t + T} {{u_L}\left( t \right)dt} \)
- \( \left\langle {{u_L}\left( t \right)} \right\rangle = \int\limits_t^{t + T} {L\frac{{di(t)}}{{dt}}dt} \)
- \( \left\langle {{u_L}\left( t \right)} \right\rangle = L\int\limits_t^{t + T} {di(t)} \)
- \( \left\langle {{u_L}\left( t \right)} \right\rangle = L\left[ {i(t)} \right]_t^{t + T} \)
- \( \left\langle {{u_L}\left( t \right)} \right\rangle = L\left[ {\underbrace {i\left( {t + T} \right) - i\left( t \right)}_0} \right] \)
- \( \left\langle {{u_L}\left( t \right)} \right\rangle = 0 \)
Énergie dans une bobine
Une bobine parfaite d'inductance L dont l'intensité du courant passe de 0 à I, emmagasine une énergie électromagnétique W :
| \( W = \frac{1}{2} \cdot L \cdot I^2 \) |
La puissance d'expression générale est \( P = ui = \frac{dE}{dt} \).
Dans une bobine la tension \( u = L \frac{di}{dt} \)
Donc la puissance prend l'expression: \( P = L \times i \frac{di}{dt} = \frac{E}{dt} \)
Et comme l'énergie est l'intégrale de la puissance dépensée
\( {W_m} = \int {L \times i\frac{{di}}{{dt}}dt} = L \times \int\limits_0^I {idi} = L \times \left[ {\frac{{{i^2}}}{2}} \right]_0^I = \frac{1}{2}L{I^2} \)
donc \( W = \frac{1}{2} \cdot L \cdot I^2 \)
Relation entre U et I, cas sinusoïdal
Si la tension et le courant dans une bobine sont sinusoïdaux, la tension et le courant sont liés par la relation
| \( \underline{U} = j L \omega \times \underline{I} \) |
Donc \( U = \left| j L \omega \right| \times \left|I\right| = L \omega \times I\)
Et \( {\varphi _U} = \underbrace {Arg(jL\omega )}_{\frac{\pi }{2}} + \underbrace {Arg(I)}_{{\varphi _I}}\)
La tension est donc déphasée de \( \frac{\pi }{2} \) par rapport au courant
et comme \( \underline{U} = \underline{Z} \times \underline{I} \)
| \( \underline{Z_L} = \frac{\underline{U}}{\underline{I}} = jL\omega \) |
| \( Z_L = jL\omega \) et \( \varphi _{Z_L} = +\frac{\pi}{2} \) |
| Valeurs instantanées:
Si le courant parcourant une bobine est sinusoïdal: \( i(t) = I\sqrt 2 \sin (\omega t) \) Comme la tension dans la bobine résulte du calcul de \(u = L\frac{di}{dt}\), Comme la dérivée de \( \sin (\omega t) \) est \( \omega \cos (\omega t) \). Et comme \( \cos (x) = \sin (x+\pi/2) \) Alors \(u(t) = L\omega I\sqrt 2 \cos (\omega t) = L\omega I\sqrt 2 \sin \left( {\omega t + \frac{\pi }{2}} \right)\) La tension est donc déphasée de \( \varphi_{U/I}= \frac{\pi}{2} \) par rapport au courant. La valeur efficace de la tension est telle que \(U= L\omega I\ \). Cet ensemble de constatation peut être résumé par la notation complexe qui lie les valeur efficace et le déphasage des grandeur u(t) et i(t): \( \underline{U} = j L \omega \underline{I} \) | 
| ||
| Construction de Fresnel:
La tension est en quadrature avance sur le courant
| 
| ||
| Impédance complexe:
\( \left| {\underline {{Z_L}} } \right| = \frac{{\left| {\underline U } \right|}}{{\left| {\underline I } \right|}} = \frac{{L\omega I}}{I} = L\omega \)
et \( \varphi_Z = \varphi_u - \varphi_i = + \pi /2 \)
soit
| 
| ||
Puissance active:
| Puissance réactive:
|
- Le rapport \( \frac{U}{I} \) ou impédance \( Z \) de la bobine est égale à \( L \omega \) et augmente avec \( \omega \) donc avec la fréquence
- une bobine se comporte donc comme un circuit ouvert à haute fréquence
- une bobine se comporte donc comme un circuit fermé en continu
- le fait de multiplier par j traduit l'avance de phase de \( \pi/2 \) du courant sur la tension donc \( \varphi_{U/I} = +\frac{\pi}{2} \)
Vidéo
Voyage en électricité Ep 20 - L'électricité en bobine (5'33") https://youtu.be/Gl-vCsOKiJc
QCM
Liens
open Classroom sur la bobine





