Vidéo
| C'est Quoi Un Condensateur? - condensateurs? 8’41’’ Mentalité Ingénieur |
| https://youtu.be/MUrG2sFIjYo |
Quelques condensateurs

Usages
Le condensateur est utilisé essentiellement pour :
- stabiliser une alimentation électrique (il se décharge lors des chutes de tension et se charge lors des pics de tension) ;
- traiter des signaux périodiques (filtrage…) ;
- séparer le courant alternatif du courant continu, ce dernier étant bloqué par le condensateur ;
- stocker de l'énergie, auquel cas on parle de supercondensateur.
- compenser l'énergie réactive d'une installation de façon à minimiser le courant absorbé
Description

Le condensateur est constitué de deux plaques conductrices de surface \( S \) en regard l'une de l'autre et séparées d'une épaisseur \( e \) par un isolant électrique de permittivité \( \epsilon \).
Lorsque deux surfaces conductrices sont placées l'une en regard de l'autre et soumises à une tension électrique, les charges électriques s'accumulent de chaque côté de l'isolant qui les sépare. Tout composant qui présente une telle propriété est un condensateur.
Plus la surface des armatures est grande, plus la charge stockée sera importante, plus l'épaisseur entre les plaques est faible, plus la charge stockée sera importante.
Plus l'isolant électrique a une forte capacité à se polariser face à un champ électrique, plus la charge stockée sera importante.
| \( C=\varepsilon_0 \varepsilon_r \frac{S}{e} \) |
- \( C \) Capacité en Farads : F
- \( \varepsilon_0 \) permittivité diélectrique du vide \( \varepsilon_0 =\frac{1}{\mu_0} c^2=8,85 \times 10^{-12} \) en \( F.m^{-1} \) . ou \( \frac{1}{36 \pi} \cdot 10^{-9} \)
- \( \varepsilon_r \) permittivité diélectrique relative (sans unités)
- \( S \) Surface en regard des armatures en \( m^2 \)
- \( e \) distance entre les armatures en \( m \)
Que se passe-t-il dans un condensateur?

Les électrons libres porteurs du courant se stockent sur les armatures du condensateur, et ne peuvent passer sur l'autre armature séparée par un isolant. La tension augmente alors tant que le courant reste présent (jusqu'au claquage de l'isolant).
la charge Q présente sur les armatures est proportionnelle à la tension et la valeur du condensateur en Farad
\( Q = C \times U \)
Symboles

Association de condensateurs
Condensateurs en parallèle:
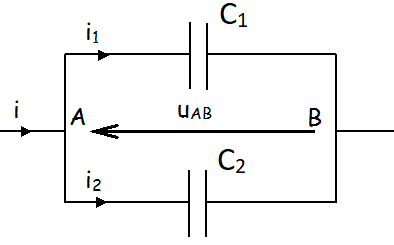
Le condensateur équivalent à des condensateurs en parallèles s'ajoutent :en effet les charges ont plus de surface pour se stocker.
| \( C_{eq}=C_1+C_2 \). |
Condensateurs en série:

| \( \frac{1}{C_{eq}}=\frac{1}{C_1}+\frac{1}{C_2} \) |
Vidéo
Voyage en électricité Ep 19 - L'électricité en sandwich (5'49")
- principe
- capacité du condensateur
https://youtu.be/2eBUTJCwmoY?start=33%%
Relation entre U et I, cas général
Quelque soit la forme de la tension ou du courant dans un condensateur, la tension et le courant sont liés par la relation
| \( i = C \frac{du}{dt} \) |
Le courant est donc le produit de la valeur du condensateur par la dérivée ou pente de la tension.
- si la tension est une sinusoïde, alors le courant sera un cosinus (soit une sinusoïde déphasée de \( \frac{\pi}{2} \)
- si la tension est en dents de scie, alors le courant est en créneaux
- si la tension est en créneaux alors des pics brutaux apparaissent sur le courant au moment de chaque transition
- si la tension est continue, la dérivée étant nulle, alors le courant sera nul, le condensateur se comporte comme un circuit ouvert.
Relation entre U et I, cas sinusoïdal
Si la tension et le courant dans un condensateur sont sinusoïdaux, la tension et le courant sont liés par la relation
| \( \underline{I} = j C \omega \times \underline{U} \) |
Donc \( I = \left| j C \omega \right| \times \left|U\right| = C \omega \times U\)
Et \( {\varphi _I} = \underbrace {Arg(jC\omega )}_{\frac{\pi }{2}} + \underbrace {Arg(U)}_{{\varphi _U}}\)
Le courant est donc déphasé de \( \frac{\pi }{2} \) par rapport à la tension donc la tension est déphasée de \( -\frac{\pi }{2} \)par rapport au courant.
et comme \( \underline{U} = \underline{Z} \times \underline{I} \)
| \( \underline{Z_C} = \frac{\underline{U}}{\underline{I}} = \frac{1}{jC\omega} = -\frac{j}{C\omega}\) |
| \( Z_C = \frac{1}{C\omega} \) et \( \varphi _{Z_C} = -\frac{\pi}{2} \) |

| Valeurs instantanées:
Si la tension alimentant un condensateur est sinusoïdal: \( u(t) = U\sqrt 2 \sin (\omega t) \) Comme le courant dans le condensateur résulte du calcul de \(i = C\frac{du}{dt}\), Comme la dérivée de \( \sin (\omega t) \) est \( \omega \cos (\omega t) \). Et comme \( \cos (x) = \sin (x+\pi/2) \) Alors \(i(t) = C\omega U\sqrt 2 \cos (\omega t) = C\omega U\sqrt 2 \sin \left( {\omega t + \frac{\pi }{2}} \right)\) Le déphasage du courant par rapport à la tension est donc \( \varphi_{I/U}= \frac{\pi}{2} \) donc la tension est déphasée de \( \varphi_{U/I}= - \frac{\pi}{2} \) par rapport au courant. La valeur efficace du courant est telle que \(I= C\omega U \). Cet ensemble de constatations peut être résumé par la notation complexe qui lie les valeur efficace et le déphasage des grandeur u(t) et i(t): \( \underline{I} = j C \omega \times \underline{U} \) | 
| ||
| Construction de Fresnel:
Le courant est en quadrature avance sur la tension
| 
| ||
| Impédance complexe:
\( \left| {\underline {{Z_C}} } \right| = \frac{{\left| {\underline U } \right|}}{{\left| {\underline I } \right|}} = \frac{U}{{UC\omega }} = \frac{1}{{C\omega }} \)
et \( \varphi_Z = \varphi_u - \varphi_i = - \pi /2 \)
soit
| 
| ||
Puissance active:
| Puissance réactive:
|
- Le rapport \( \frac{U}{I} \) ou impédance \( Z \) du condensateur est égal à \( \frac{1}{C \omega} \) et diminue avec \( \omega \) donc avec la fréquence
- un condensateur se comporte donc comme un circuit fermé à haute fréquence
- un condensateur se comporte donc comme un circuit ouvert en continu
- le fait de multiplier par j traduit l'avance de phase de \( \pi/2 \) de la tension sur le courant donc \( \varphi_{U/I} = -\frac{\pi}{2} \)
Énergie dans un condensateur
Un condensateur parfait de capacité C dont la tension passe de 0 à U, emmagasine une énergie électromagnétique W :
| \( W = \frac{1}{2} \cdot C \cdot U^2 \) |
La puissance d'expression générale est \( P = ui = \frac{dE}{dt} \).
Dans un condensateur le courant \( i = C \frac{du}{dt} \)
Donc la puissance prend l'expression: \( P = C \times u \frac{du}{dt} = \frac{E}{dt} \)
Et comme l'énergie est l'intégrale de la puissance dépensée
\( {W_m} = \int {C \times u \frac{du}{dt}dt} = C \times \int\limits_0^U {udu} = C \times \left[ {\frac{{{u^2}}}{2}} \right]_0^U = \frac{1}{2}C{U^2} \)
donc \( W = \frac{1}{2} \cdot C \cdot U^2 \)
Technologies des condensateurs
Il est composé de deux électrodes métalliques séparées par un isolant. Ce système est réalisé soit par des feuilles enroulées, empilées ou placées de manière tubulaire. Une métallisation d'une plaquette de céramique est également une technique utilisée. Ils sont protégés des influences extérieures par une couche de vernis, un enrobage de masse isolante (résine) ou un boîtier d'aluminium. voir aussi : http://www.composelec.com/condensateur_(electricite).php
Mesure d'un condensateur
- A l'aide d'un capacimètre
- par une mesure des tension, courant et déphasage lors de l'alimentation du condensateur à une fréquence donnée
Caractéristiques des condensateurs
- Capacité nominale \( C \) [F],
- Tension de service [V]: tension normale d'usage
- Tolérance [%]: tolérance de précision de la capacité
- coefficient de températures [1/K].
- Facteur de pertes \( tan \delta \) donne l'énergie perdue en en regard de l'énergie réactive fournie
Le condensateur est caractérisé par l’angle de perte \( \delta \) et sa tangente qui augmente avec les imperfections.
Les fabricants nous donnent le facteur de pertes qui est en fait le rapport de la puissance perdue avec la puissance réactive.

sources web
- http://www.epsic.ch/cours/electronique/techn99/elnthcomp/condthtxt.html
- http://www.composelec.com/condensateur_(electricite).php
- https://fr.farnell.com/capacitor-types-and-performance
- https://f5zv.pagesperso-orange.fr/RADIO/RM/RM24/RM24G/RM24G.HTM
- achats:





