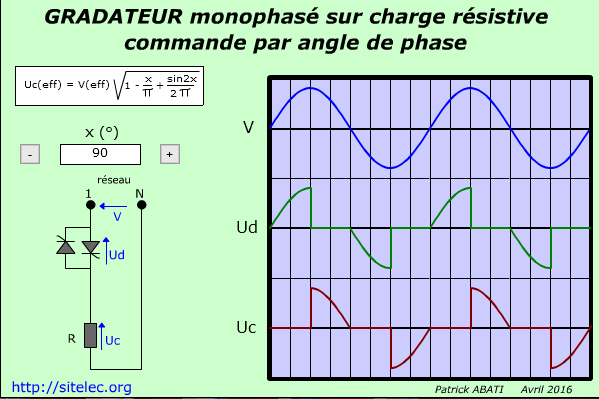
Courbes
- A \( t_o \), \( T_1 \) reçoit une impulsion. Il est alors polarisé en direct (alternance >0 de \( v(t) \)). Il s’amorce. \( u_c = v(t) = V_{max} sin \omega t>0 \).
- A \( T/2 \), \( v(t)=u_c=0 \), \( i_c=0 \). Le thyristor \( T_1 \) se bloque.
- A \( t_o+ T/2 \), \( T_2 \) reçoit une impulsion. Il est alors polarisé en direct (alternance <0 de \( v(t) \)). Il s’amorce. \( u_c = v(t) = V_{max} sin \omega t < 0 \).
- A T, \( v(t)=u_c=0 \), \( i_c=0 \). Le thyristor \( T_2 \) se bloque.
- \( u_T=0 \) quand \( T_1 \) ou \( T_2 \) conduisent.
- \( U_T = v-u_c = u \) quand \( T_1 \) et \( T_2 \) sont bloqués.
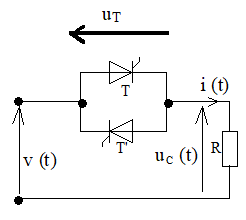 | 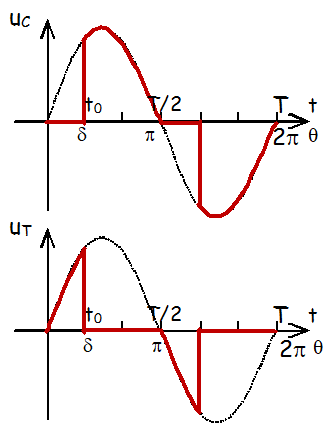 |
Détermination des grandeurs
La valeur efficace est définie par: \( {U_C} = \sqrt {\frac{1}{\pi }\int\limits_\delta ^\pi {u_c^2\left( \theta \right)d\theta } } =\sqrt {\frac{1}{\pi }\int\limits_\delta ^\pi {\left( {\sqrt 2 \times V\sin \left( \theta \right)} \right)^2 d\theta } } = \sqrt {\frac{1}{\pi }\int\limits_\delta ^\pi {2{V^2}{{\sin }^2}\left( \theta \right)d\theta } } \)
En utilisant \( {\sin ^2}\left( \theta \right) = \frac{{1 - \cos 2\theta }}{2} \)
On obtient \( {U_C} = V\sqrt {\frac{1}{\pi }\int\limits_\delta ^\pi (1 - \cos 2\theta d\theta ) } = V\sqrt {\frac{1}{\pi }\left[ {\theta - \frac{{\sin 2\theta }}{2}} \right]_\delta ^\pi } \)
Soit
| \( {U_C} = V\sqrt {1 - \frac{\delta }{\pi } + \frac{{\sin 2\delta }}{{2\pi }}} \) |
et comme \( I=\frac{U}{R} \)
Alors
| \( P = \frac{{U_C}^2}{R } = \left( {\frac{{{V^2}}}{R}} \right)\left( {1 - \frac{\delta }{\pi } + \frac{{\sin 2\delta }}{{2\pi }}} \right) \) |

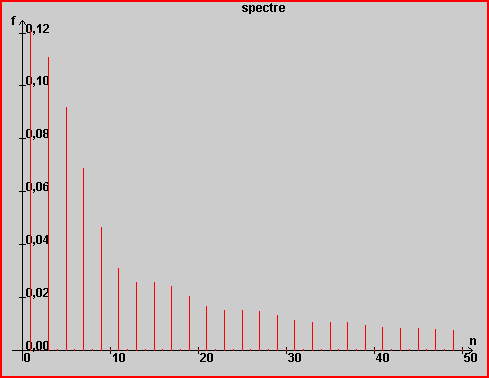
Spectres
Spectre du courant et de la tension
| pour \( \delta=50 \% \) | pour \( \delta=80 \% \) |
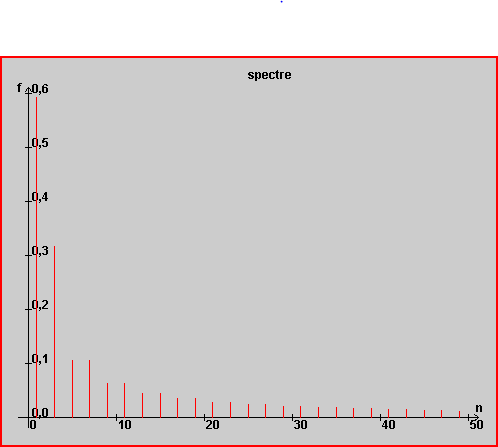
| 
|