Schéma
L'étude du gradateur triphasé va se faire avec une charge purement résistive en étoile sans neutre neutre relié.
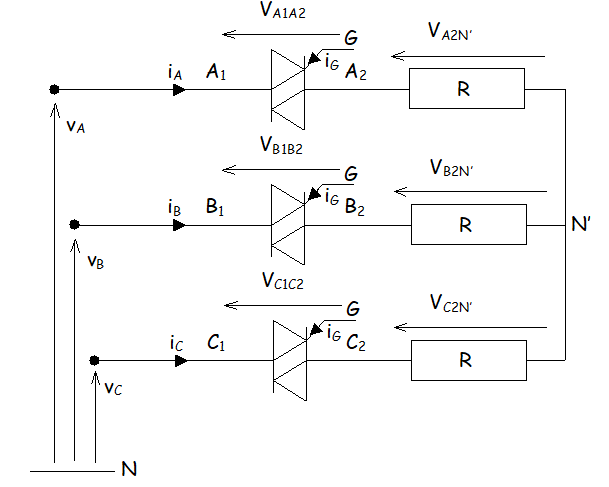
Possibilités de conduction :
Suivant les modes de commande trois cas sont possibles :
- Un interrupteur est commandé :
Pas de conduction du courant possible (pas de boucle pour le courant)
- Deux interrupteurs sont commandés :
Exemple : Interrupteurs a et b commandés : la tension Uab alimente les deux résistances.
- Trois interrupteurs sont commandés :
L’installation correspond alors à une installation triphasée équilibrée. \( V_N=V_N’=0 \), la tension sur un élément est alors une tension simple
Influence de \( \delta \)
Suivant la valeur de l'angle de retard à l'amorçage \( \delta \), le mode de fonctionnement est différent
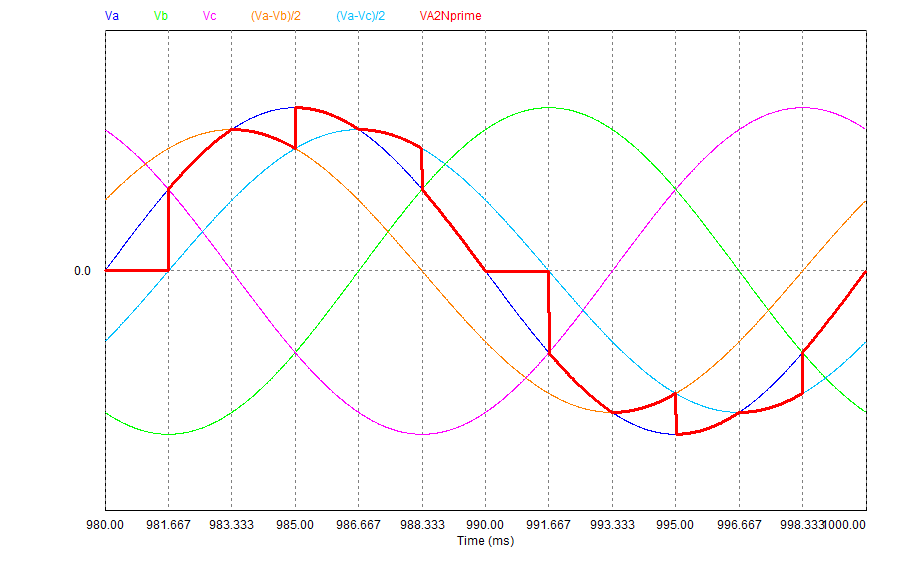
Cas où : \( 0 < \delta < \pi/3 \) :
\( u_{Ca} = v_a = R i_a \) ;
\( u_{Cb} = v_b = R i_b \) ;
\( u_{Cc} = v_c = R i_c \) ;
\( u_{Ta} = u_{Tb} = u_{Tc} = 0 \) ;
\( u_{Ca} = - u_{Cb} = \frac{1}{2} (v_a - v_b) \) ; \( i_a = - i_b = `\frac{u_{Ca}}{R} \) ; \( u_{Cc} = R i_c = 0 \).
\( u_{Ta} = u_{Tb} = 0 \) et \( u_{Tc} = \frac{3}{2} v_c < 0 \).
| 
|
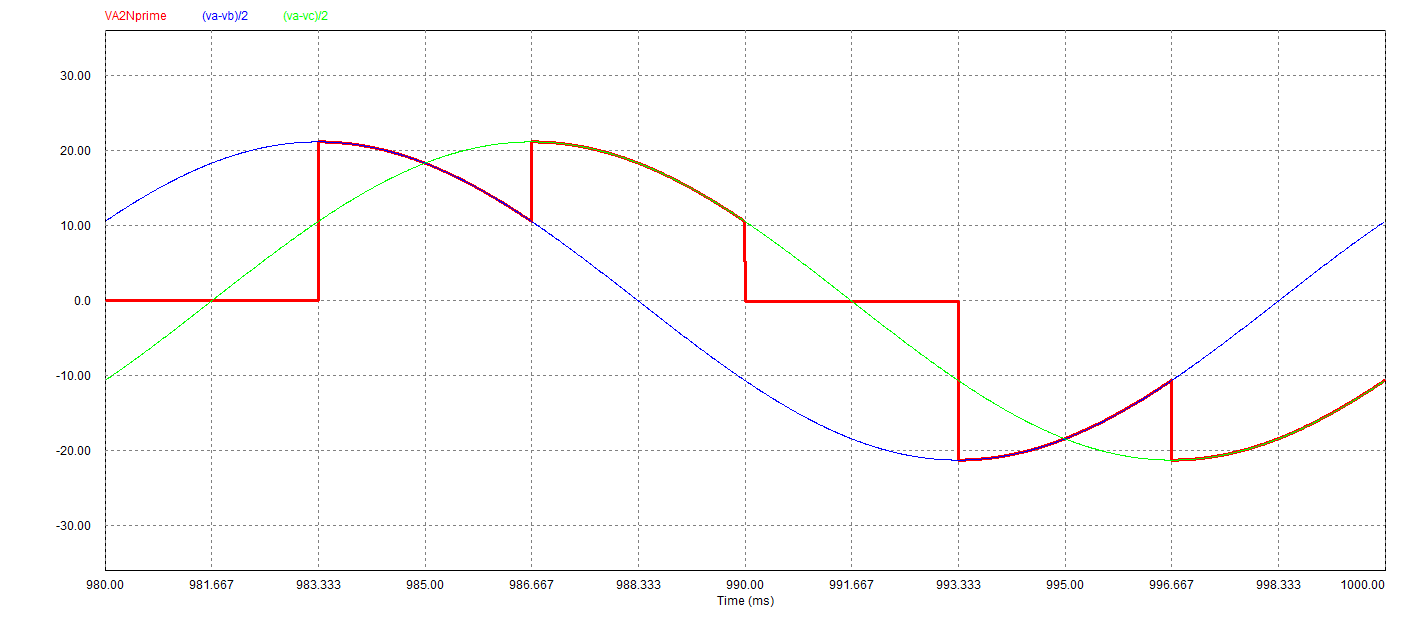
| Cas où : \( \pi/3 < \delta < \pi/2 \) :
On a toujours deux thyristors passants,
\( u_{Ca} = -u_{Cb} = \frac{1}{2}(V_a - V_b) \) ;
\( i_{a} = -i_b = \frac{u_{Ca}}{R} \) ;
\( u_{Cc} = R i_c = 0 \) ;
\( u_{Ta} = u_{Tb} \) et \( u_{Tc} = \frac{3}{2} v_c < 0 \) ;
| 
|
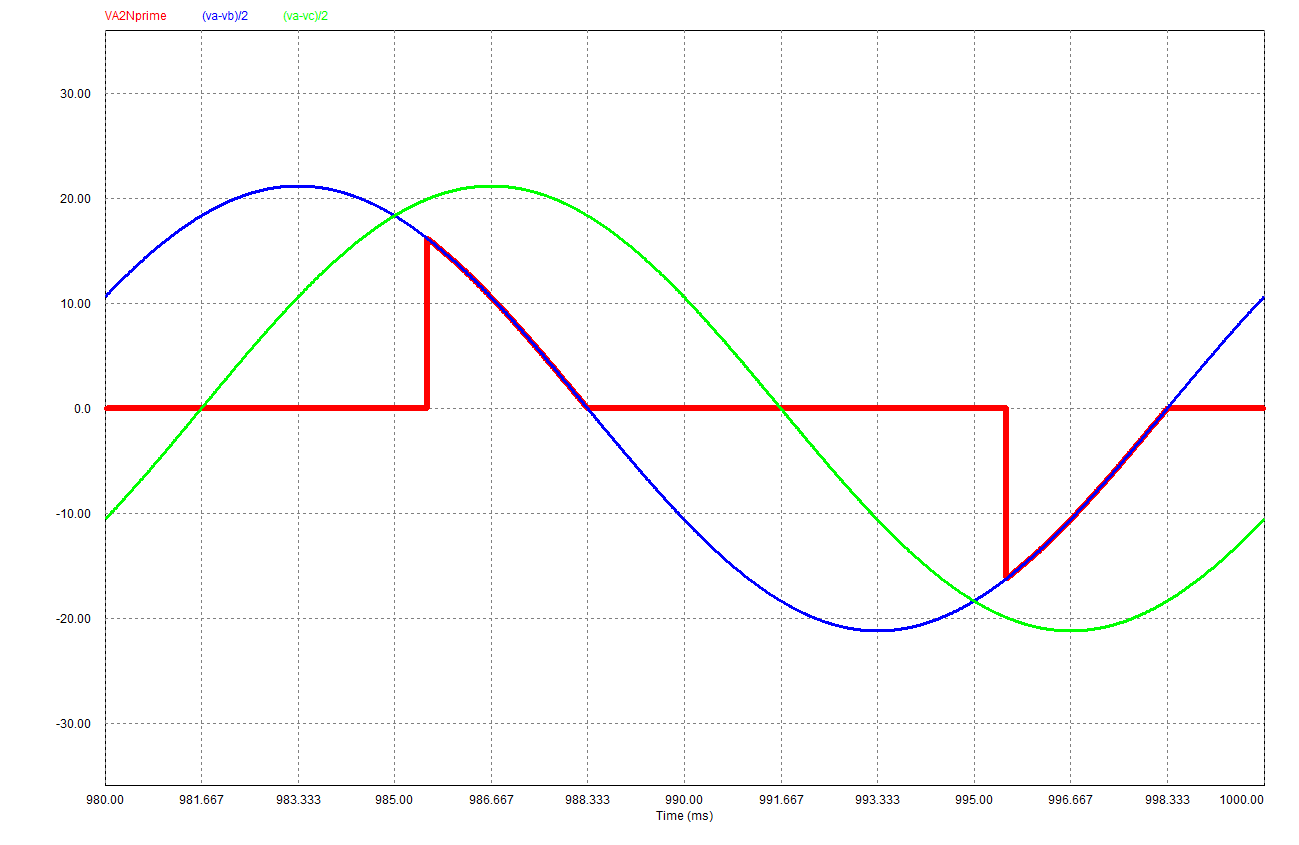
| Cas où : \( \pi/2 < \delta < 5\pi/6 \) :
Dans ce cas on a la conduction de deux thyristors ou aucun, donc, il faut amorcer deux thyristors à chaque fois. Les signaux envoyés ont une largeur supérieure à \( \pi/3 \) sur les gâchettes, ou bien on envoie une impulsion par exemple sur la gâchette de \( T_a \) à \( \theta = \delta \), puis une deuxième impulsion (pour la confirmation) à {$ \theta = \delta + \pi/3} .
\( u_{Ca} = -u_{Cb} = \frac{1}{2}(v_a - v_b) \) ;
\( i_a = -i_b = \frac{u_{Ca}}{R} \) ;
\( u_{Cc} = R i_c =0 \) ;
\( u_{Ta} = u_{Tb} = 0 \) et \( u_{Tc} = \frac{3}{2} v_c < 0 \) ;
\( u_{Ca} = u_{Cb} = u_{Cc} = 0 \) ; \( i_a = i_b = i_b =0 \) ; \( u_{Ta} - u_{Tc} = v_a -v_c > 0 \).
| 
|





