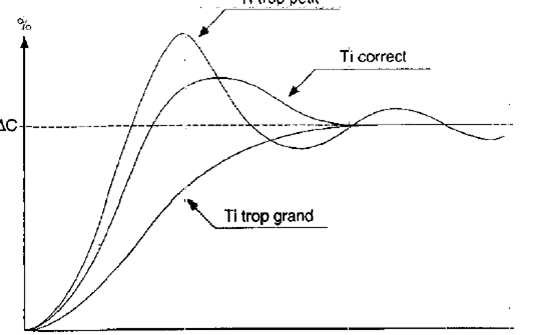
Modalité de l’action intégrale:
Le signal de commande est proportionnel à l’intégrale du signal d’erreur
\( X_e = {1 \over {T_i }}\int\limits_{ - \infty }^t {\varepsilon (t)dt} = {1 \over {T_i }}\int\limits_0^t {\varepsilon (t)dt} + \underbrace {{1 \over {T_i }}\int\limits_{ - \infty }^0 {\varepsilon (t)dt} }_{X_{e0} }\)
et la fonction de transfert isomorphe \( C(p) = {{X_e (p)} \over {\varepsilon (p)}} = {1 \over {T_i p}} \)
Il s’emploie en combinaison avec une action proportionnelle. \( C(p) = {{X_e (p)} \over {\varepsilon (p)}} = K_p + {1 \over {T_i p}} \)
Ce filtre intervient aux fréquences basses (régime permanent) (\( p=j\omega \) petit donc \( {1 \over {T_i p}}\) grand donc l’action de \( C(p) \) est grande).
Il n’intervient pas aux fréquences élevées ce qui correspond aux régimes transitoires (\( p=j\omega \) grand donc \( {1 \over {T_i p}}\) petit donc l’action de \( C(p) \) est faible).
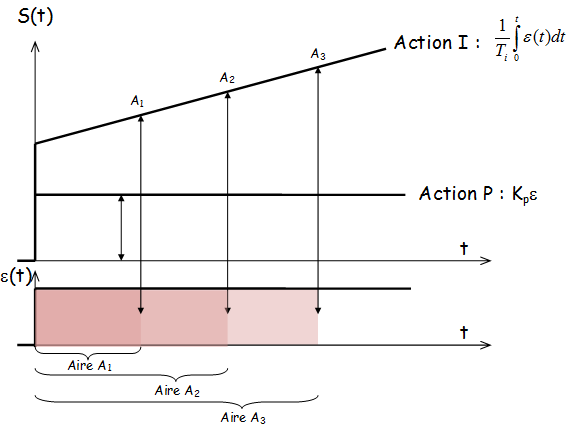
Avantages et inconvénients de l’action intégrale:
Il joue sur la précision en éliminant l’erreur en régime permanent (élimine l’erreur statique ) Il augmente la rapidité et augmente l’instabilité.

Influences d’un correcteur proportionnel intégral dans les diagramme de Bode et Nyquist
- Plus l’action intégrale est élevée (Ti petit), plus la réponse s’accélère et plus la stabilité se dégrade (réponse forte à une petite erreur) .
- Il permet de filtrer les variables bruitées (HF) ( \({1 \over {T_i p}}\) petit si \( p=j\omega \) grand)
- Il faut également trouver un bon compromis entre vitesse et stabilité.
- Dans les régulateurs industriels on affiche 1/Ti, alors \( T_i \) est d’autant plus grand que l’action intégrale est faible.
- Pas d'action Intégrale : \( T_i \) infini