En monophasé
Dans un circuit alimenté sous une tension sinusoïdale de fréquence constante, la puissance active totale :\( P_{tot} \) dissipée dans un groupement de dipôles est égale à la somme des puissances actives dissipées par chaque dipôle.
Il en est de même pour la puissance réactive : \( Q_{tot} \).
La connaissance de la puissance active totale et de la puissance réactive totale permet de connaître la puissance apparente totale \( S_{tot} \) de l'installation et d'en déduire le courant consommé .
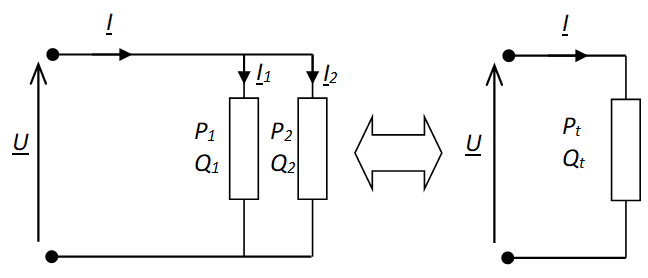 Charges en parallèle 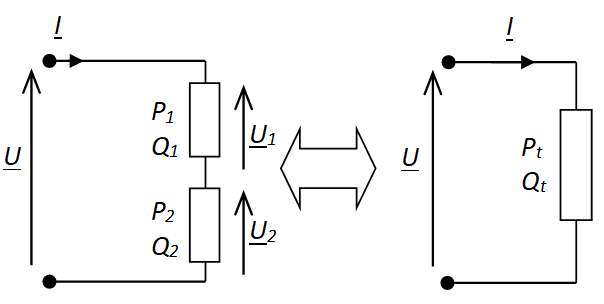 Charges en série |
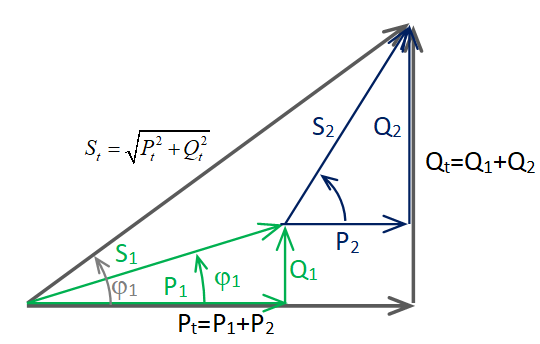 |
Ceci peut se résumer par :
| \( P_{tot} = P_1 + P_2 + ... = \sum\limits_{i = 1}^{i = n} {P_i}\) |
| \( Q_{tot} = Q_1 + Q_2 + ... = \sum\limits_{i = 1}^{i = n} {Q_i}\) |
La puissance apparente \( S_{tot} \) de l’ensemble n’est pas la somme des puissances apparentes.
On calcule d’abord \( P_{tot} = \sum\limits_{i = 1}^{i = n} {P_i} \) et \( Q_{tot} = \sum\limits_{i = 1}^{i = n} {Q_i} \) on déduit la puissance apparente de l’ensemble avec le triangle des puissances: \( S = \sqrt {P_{tot}^2 + Q_{tot}^2} \)
En monophasé: chaque dipôle est alimenté par une tension simple V
| \( P_{tot} = \sum\limits_{i = 1}^{i = n} {P_i} = VI cos \varphi \) |
| \( Q_{tot} = \sum\limits_{i = 1}^{i = n} {Q_i} = VI sin \varphi \) |
On détermine ensuite la puissance apparente qui dépend des puissances active et réactive totales:
| \( S_{tot} = \sqrt{P_{tot}^2 +Q_{tot}^2} \) |
On détermine ensuite à l'aide de la définition de la puissance apparente en monophasé \( S=V \times I \) le courant consommé par l'ensemble de l'installation:
| \( \Rightarrow I = \frac{S}{V} \) |
Le facteur de puissance de l'installation est donné par
| \( f_P = \frac{P_{tot}}{S_{tot}} \) |
En triphasé
En triphasé équilibré
En triphasé:
| \( P_{tot} = \sum\limits_{i = 1}^{i = n} {P_i} = \sqrt{3} UI cos \varphi \) |
| \( Q_{tot} = \sum\limits_{i = 1}^{i = n} {Q_i} = \sqrt{3} UI sin \varphi \) |
La puissance apparente est toujours déterminée par
| \( S= \sqrt{ P_{tot}^2 + Q_{tot}^2 } \) |
le bilan est donc identique mais en triphasé
| \( S= 3 \times V \times I = \sqrt{3} U \times I \) |
Le courant consommé par l'ensemble de l'installation est donc donné par:
| \( \Rightarrow I = \frac{S}{\sqrt{3} \times U} = \frac{S}{3 \times V} \) |
Le facteur de puissance de l'installation est donc
| \( f_P = \frac{P_{tot}}{S} \) |
Remarque : Le théorème de Boucherot basé sur la séparation des puissances active et réactive permet en régime sinusoïdal une autre méthode d'étude des circuits électriques.
En triphasé déséquilibré
Généralement un système comporte des charges mono et tri. Pour le bilan de puissance tu peux opter pour deux solutions :
- La puissance des charges mono est négligeable alors tu négliges.
- Tu réalises le bilan de puissance phase par phase.





