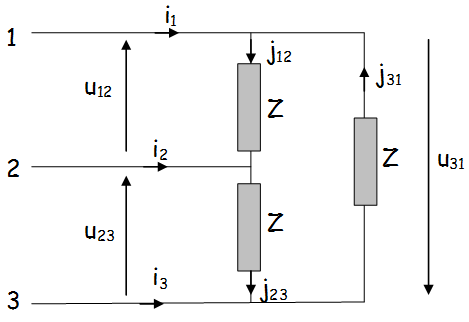
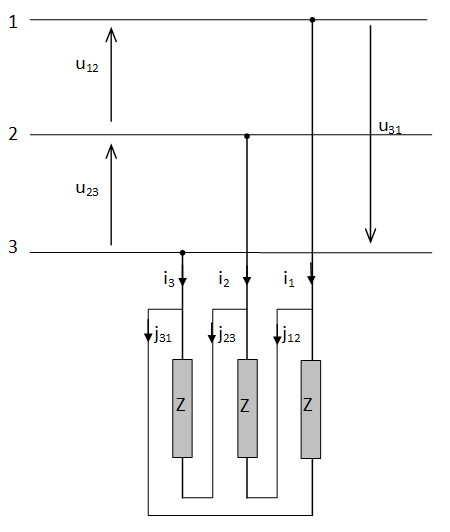
Montage triangle équilibré
Chaque phase du récepteur est soumise à une tension composée:
\({J_{12}} = {J_{23}} = {J_{31}} = J = \frac{U}{Z}\)
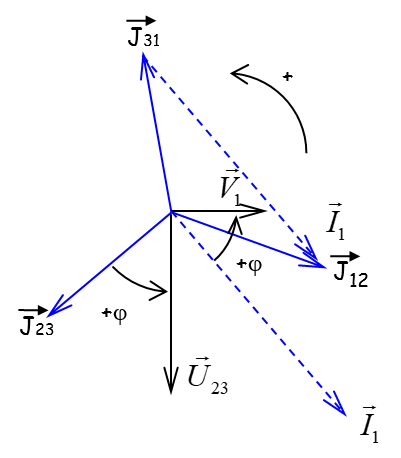
L’angle \( \varphi \) entre U et J est imposé par la charge
Les relations liant les courants par phase et en ligne sont :
\(\left. \begin{array}{l} {i_1} = {j_{12}} - {j_{31}} \\ {i_2} = {j_{23}} - {j_{12}} \\ {i_3} = {j_{31}} - {j_{23}} \\ \end{array} \right\} \Rightarrow {I_1} = {I_2} = {I_3} \)
Par une démonstration analogue à celle pour les tensions, on trouve le second résultat important
| \(I = J\sqrt 3 \) |
Le courant de ligne \( I \) dans une installation triphasée équilibrée couplée en triangle est égal à \( \sqrt 3 \times J \) soit racine de 3 fois le courant dans une branche liant 2 phases.
|
\( \left\{ \begin{array}{l} {{\underline J}_{12}} = \frac{{{{\underline U}_{12}}}}{{\underline Z}} = \frac{U}{Z}{e^{j\left( {\omega t - \varphi + \frac{\pi }{6}} \right)}} \\ {{\underline J}_{23}} = \frac{{{{\underline U}_{23}}}}{{\underline Z}} = \frac{U}{Z}{e^{j\left( {\omega t - \varphi - \frac{\pi }{2}} \right)}} \\ {{\underline J}_{31}} = \frac{{{{\underline U}_{31}}}}{{\underline Z}} = \frac{U}{Z}{e^{j\left( {\omega t - \varphi - \frac{{7\pi }}{6}} \right)}} \\ \end{array} \right. \) |
  |
 |
Remarque : A chaque instant \( i_1+i_2+i_3=0\) et \( j_{12}+j_{23}+j_{31}=0 \)
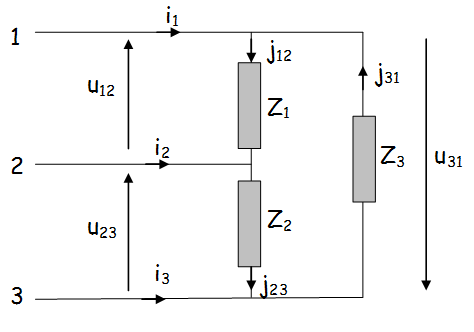
Montage triangle déséquilibré
Les récepteurs différents sont reliés entre deux fils de phase, les courants dans chaque récepteur sont différents en phase et en valeur.
|
\(\left\{ \begin{array}{l} {{\underline J}_{12}} = \frac{{{{\underline U}_{12}}}}{{{{\underline Z}_1}}} = \frac{U}{{{Z_1}}}{e^{j\left( {\omega t - {\varphi _1} + \frac{\pi }{6}} \right)}} \\ {{\underline J}_{23}} = \frac{{{{\underline U}_{23}}}}{{{{\underline Z}_2}}} = \frac{U}{{{Z_2}}}{e^{j\left( {\omega t - {\varphi _2} - \frac{\pi }{2}} \right)}} \\ {{\underline J}_{31}} = \frac{{{{\underline U}_{31}}}}{{{{\underline Z}_3}}} = \frac{U}{{{Z_3}}}{e^{j\left( {\omega t - {\varphi _3} - \frac{{7\pi }}{6}} \right)}} \\ \end{array} \right.\) \( \begin{array}{l} {\overrightarrow I _1} = {\overrightarrow J _1} - {\overrightarrow J _3} \\ {\overrightarrow I _2} = {\overrightarrow J _2} - {\overrightarrow J _1} \\ {\overrightarrow I _3} = {\overrightarrow J _3} - {\overrightarrow J _2} \\ \end{array} \) |
 |
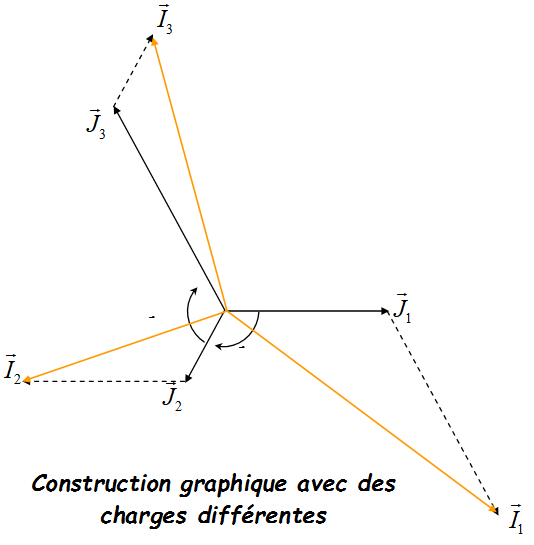 |
La somme des courants dans les fils de ligne est nulle : \( \overrightarrow {{I_1}} + \overrightarrow {{I_2}} + \overrightarrow {{I_3}} = \overrightarrow 0 \)





