On raisonne comme si le transformateur triphasé au secondaire était composé de trois transformateurs monophasés où le secondaire serait monté en étoile. On utilise alors le modèle du transformateur monophasé où la résistance et l’inductance de fuite primaires sont ramenées au secondaire.
Le modèle ci-dessous est celui de la phase A. Les tensions secondaires \( V_a \) , \( V_b \) , \( V_c \) sont modifiées lorsque le transformateur est chargé. Pour la phase a, on introduit \( V_{20} \) tension à vide phase neutre ce qui permet de faire intervenir l’indice horaire.
- Le rapport de transformation \( m \) est toujours tel que \( V_{20} = m{V_1} \), le rapport m dépendant du type de couplage
- Comme le couplage amène un déphasage entre le primaire et le secondaire, l'expression complexe qui prend en compte le déphasage est donc: \( \underline V_{20} = m{\underline V_1} \cdot {e^{j\alpha }}\) avec \(\alpha = \left( {\widehat{{{\vec V}_A},{{\vec V}_{a0}}}} \right) = 2\pi - h \times \frac{\pi }{6}\)
donc
| \({\underline V_{20}} = m \cdot {e^{ - jh\frac{\pi }{6}}}{\underline V_1}\) |
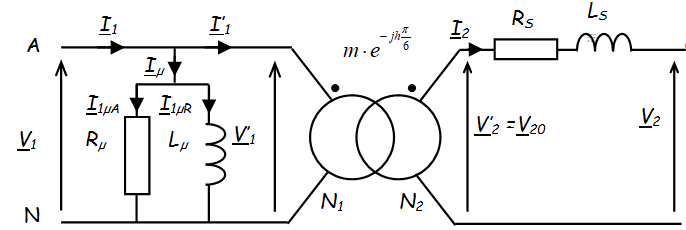
Modèle équivalent d'une phase du transformateur triphasé
Les différences avec le modèle du transformateur monophasé sont:
- La prise en compte du déphasage entre le primaire et le secondaire par le biais de l'indice horaire
- Le modèle est celui d'une seule phase ( il faudra donc multiplier par 3 pour avoir les pertes)





