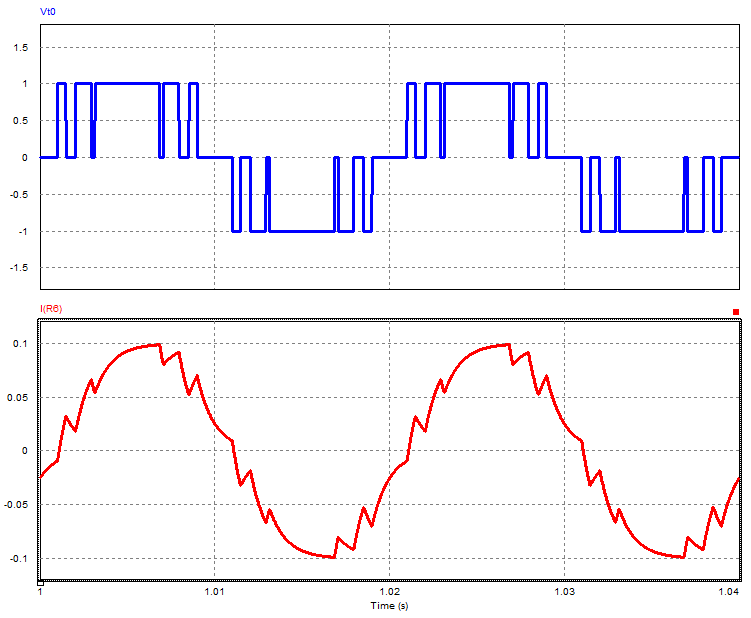
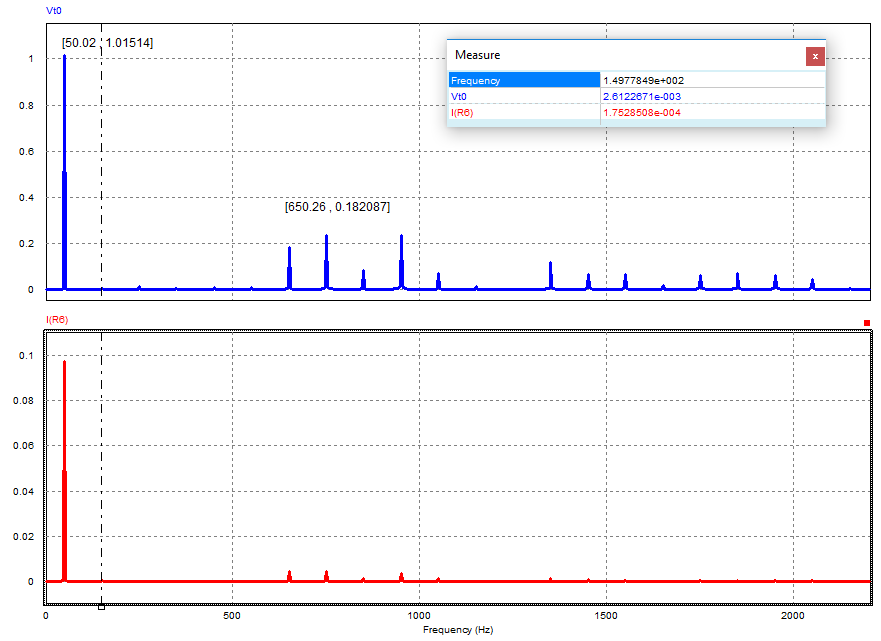
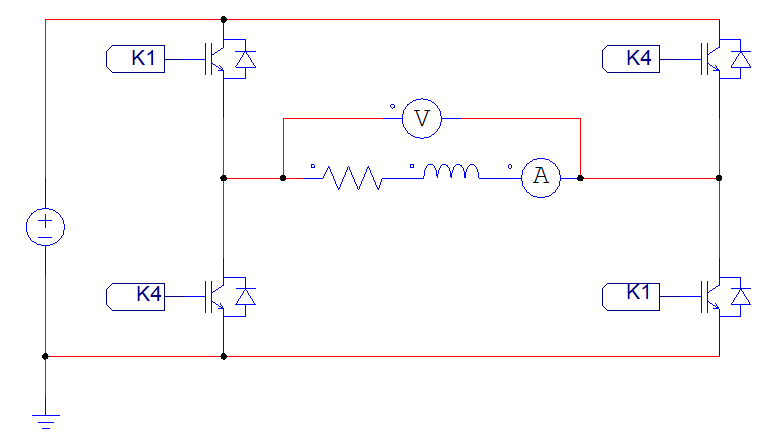
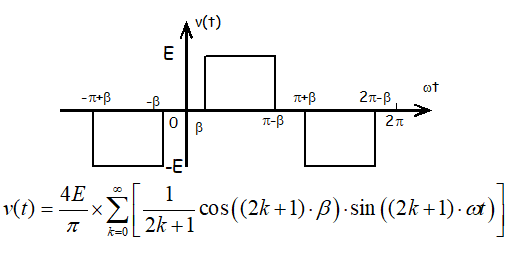
On cherche à éliminer les harmoniques de faibles rang .On élimine les harmoniques de rang 3f,5f,7f… par l’introduction de fentes dans une forme d’onde rectangulaire.
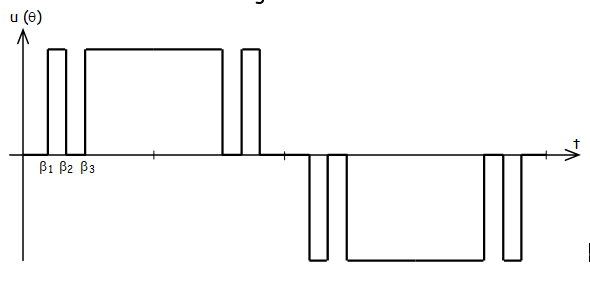
Il faut déterminer les angles b1, b2, b3…. b5.
On considère que u est la somme algébrique de forme d’onde en créneaux du type :
 |
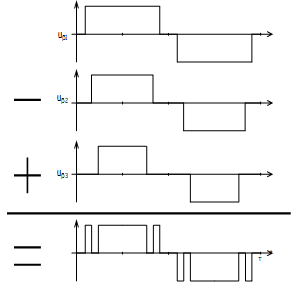 |
\( u(\theta)=u_{\beta 1}+u_{\beta 3}+u_{\beta 5}-u_{\beta 2}-u_{\beta 4} \)
Dans l’expression ci-dessus, pour éliminer les harmoniques n, il faut
\( cos n{\beta 1}+ cos n{\beta 3}+ cos n{\beta 5}- cos n{\beta 2}- cos n{\beta 4}=0 \)
5 angles donc 5 équations sont nécessaires.
La résolution donne :
\( {\beta 1}=18,17°, {\beta 2}=26,64°, {\beta 3}=36,87°,{\beta 4}=52,9°, {\beta 5}=56,69°. \)
Dans ce cas là, \( U_{eff} \) est fixe et dépend de \( {\beta 1}, {\beta 2}, {\beta 3}, {\beta 4}, {\beta 5} \)
Voir :BTS Et 2000 Nouméa