Point Fonctionnement

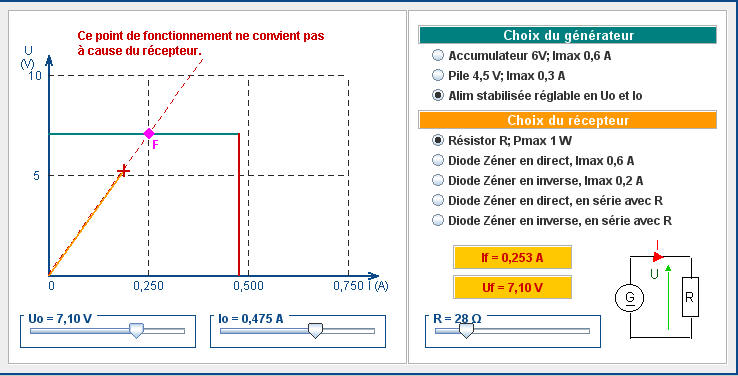
Domaines d'utilisation

La notion de point de fonctionnement est vaste et s'applique à de nombreux domaines. Parmi ceux qui nous préoccupent, on retiendra

• le point de fonctionnement électrique entre un générateur et sa charge
• le point de fonctionnement mécanique entre un moteur et la charge entrainée

Domaines d'utilisation

Le point de vue mécanique permet de comprendre ce qu'est le point de fonctionnement.

• Si on considère un cycliste qui essaye de donner toujours son maximum et qu'on observe sa vitesse: ce sera notre générateur
• Si ce cycliste est placé sur une route plate: c'est notre charge 1.
• Le cycliste atteint une certaine vitesse: c'est un premier point de fonctionnement
• Si ce cycliste est placé sur une route montante: c'est notre charge 2.
• Le cycliste atteint une autre vitesse, plus faible: c'est un deuxième point de fonctionnement

Pour un générateur électrique, c'est pareil, sa tension (que l'on pourrait comparer à la vitesse du cycliste) va baisser au fur et a mesure qu'on lui demande du courant (comparable à la cote de la route).

Point de vue graphique

Les générateurs de tension sont des éléments qui sont capable de fournir une certaine tension si on ne leur demande pas de courant, mais dont la tension baisse lorsque le courant demandé augmente. La variation de la tension du générateur \( U_G \) en fonction de \( I_G \) : \( U_G=f(I_G) \) décrit donc une courbe, qui peut être une droite ou non.

Le récepteur possède lui aussi des exigences qui sont telles que à une certaine tension le traversant, un certain courant le traversera \( U_R=f(I_R) \).

Lorsqu'on branchera la charge sur le générateur, le point de fonctionnement sera le point d'intersection de ces deux courbes car

• le courant débité par le générateur est reçu par le récepteur donc \( I_G=I_r \)
• la tension présente aux bornes du générateur est présente sur le récepteur donc \( U_G=U_r \)

Point de vue mathématique

• Le récepteur présente une équation qui décrit sa variation de tension en fonction du courant qui le traverse \( U_R=f(I_R) \)
• Le générateur présente une équation qui décrit sa variation de tension en fonction du courant qu'il fournit\( U_G=f(I_G) \)
• l'intersection de ces deux courbes se trouve en résolvant le système à deux équations ainsi créé

Exemple:

• \( U_R=f(I_R) \) donne \( U_R=5 \times I_R \)
• \( U_G=f(I_G) \) donne \( U_G=10 - 2 \times I_G \)

On peut remplacer \( U_R \) et \( U_G \) par \( U \) et \( I_R \) et \( I_G \) par \( I \)
On a donc bien deux équations à deux inconnues.

• \( U=5 \times I \)
• \( U=10 - 2 \times I \)

Pour résoudre ce système d'équation, il suffit dans ce cas d'égaliser les deux équations donc
\( 5 \times I = 10 - 2 \times I \)
puis
\( 5 \times I + 2 \times I= 10 \)
\( 7 \times I = 10 \)
\( I = 10/7 \)

Auto-évaluation

• Lycée Charles Augustin Coulomb: Exercice