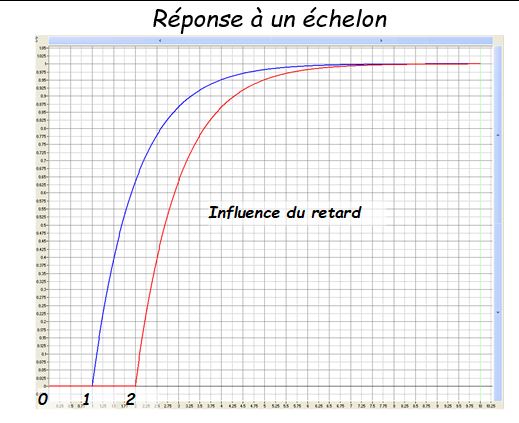
Lorsque la réponse à un échelon du système en boucle ouverte ne présente pas de rebond mais qu’il existe un retard entre l’échelon et la réponse, le modèle de Broïda peut être utilisé.
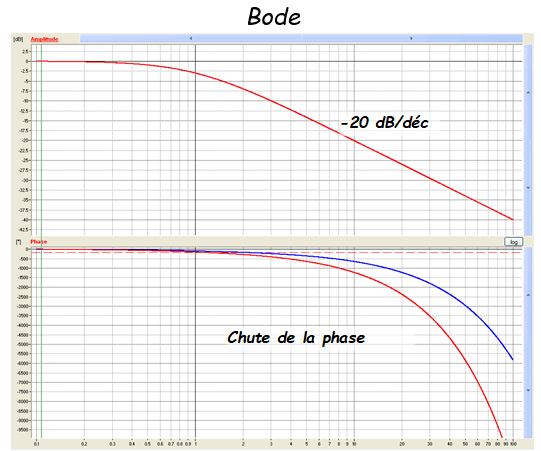
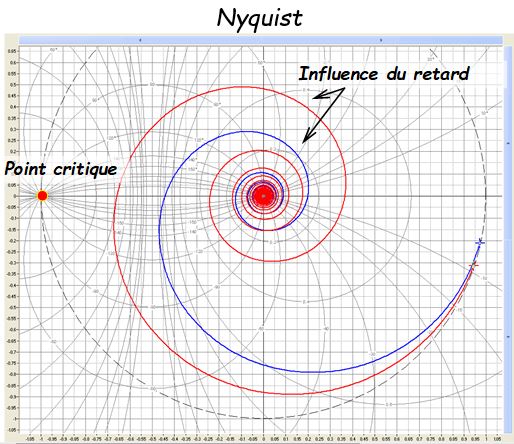
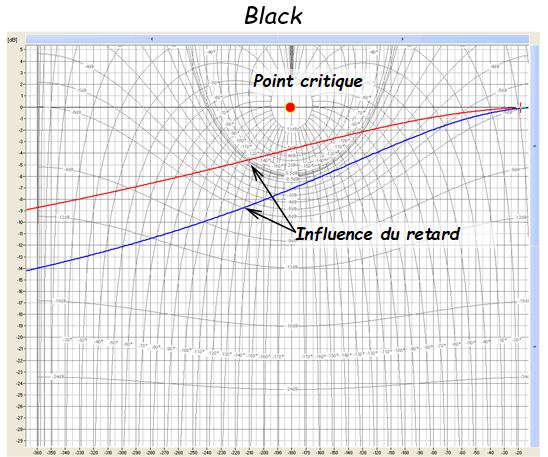
La fonction de transfert isomorphe est alors décrite de la façon suivante: \( H(p) = \frac{{K{e^{ - Tp}}}}{{1 + \tau p}} \)
Cette fonction de transfert fait apparaître une fonction du premier ordre de gain \( k \) est de constante de temps \( \tau \) couplée à une fonction retard de temps \( T \)
- Avec \( K \) le gain statique toujours défini comme \( K= \frac{\Delta{s}}{\Delta{e}} \)
- La constante de temps \( \tau \) est souvent prise égale à la pente au point d’inflexion, mais une méthode plus précise préconise de
-relever le temps \( t_1 \) au bout duquel on atteint \( 28\% \) de \( \Delta{s} \)
-relever le temps \( t_2 \) au bout duquel on atteint \( 40\% \) de \( \Delta{s} \)
-la constante de temps \( \tau \) est donné par \( \tau=5,5 \cdot (t_2 -t_1) \)
-le retard \( T \) est donné par \( \tau=2,8 \cdot t_1 - 1,8 \cdot t_2 \)
Plus le retard est grand plus, le décalage dans le temps de la fonction est grand.
