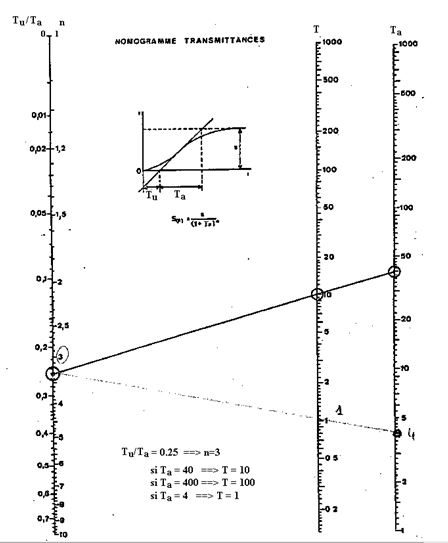
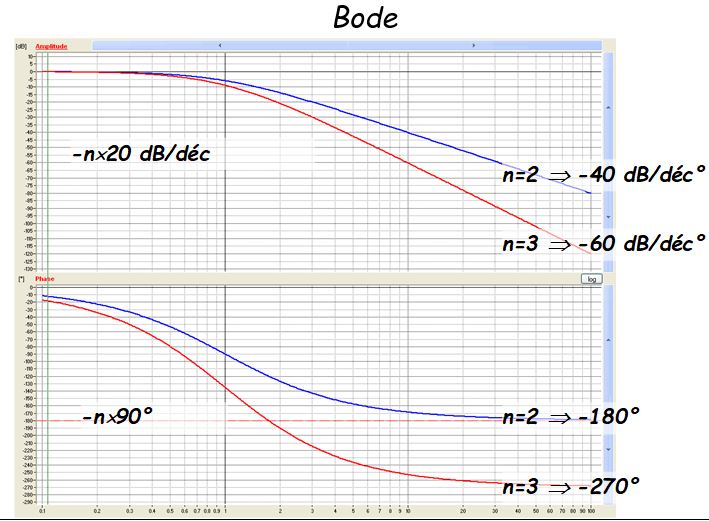
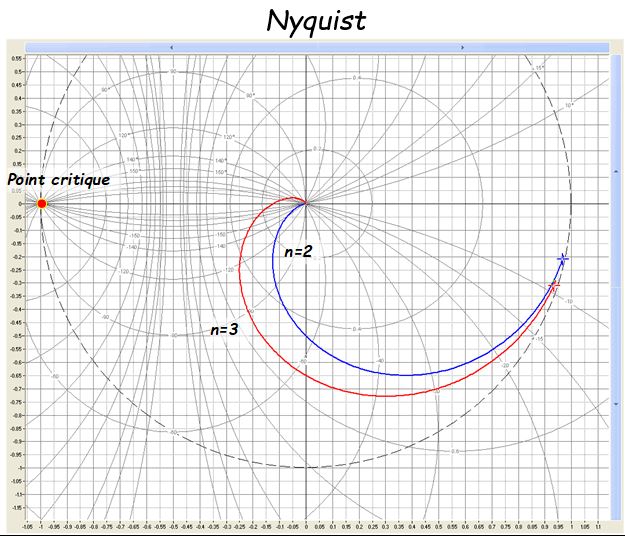
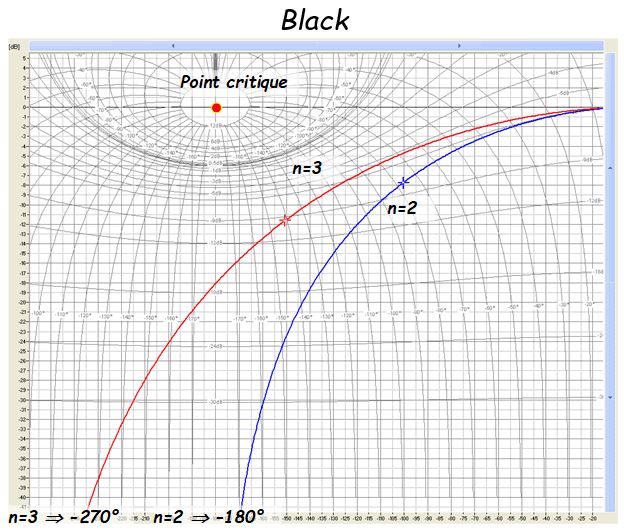
Fonction de transfert isomorphe : \( H(p) = \frac{{K{e^{ - \tau p}}}}{{{{\left( {1 + Tp} \right)}^n}}} \) ; \( \tau \) étant le retard
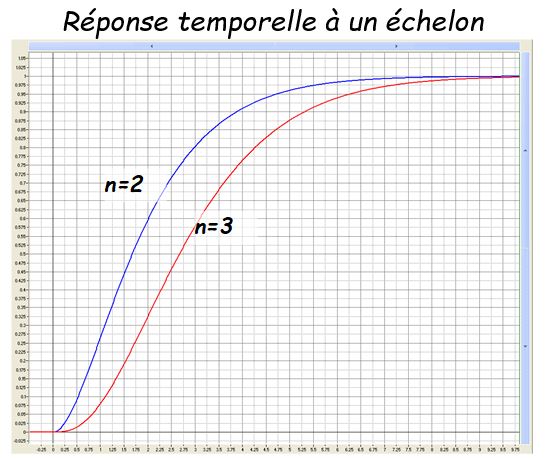
Si l'on trace la droite tangente au point d'inflexion de la courbe de réponse
- la droite tangente coupe l'abscisse au temps \( T_u \)
- la droite tangente coupe la valeur asymptote de la courbe de réponse au temps \( T_u + T_a \)
Alors le nomogramme suivant permet de connaitre la puissance \( n \) du polynôme et la grandeur \( T \).