
Lorsqu'on ne dispose que d'un seul Wattmètre, il est possible par deux mesures de mesurer les puissances active et réactive d'une charge triphasée équilibrée.
Si la charge est déséquilibrée seule la mesure de puissance active est valable avec cette méthode.
Pour la puissance active (charge triphasée équilibrée ou non)
Les deux wattmètres mesurent \(M_{13}^1 = \left\langle {\left( {v_1 - v_3 } \right)i_1 } \right\rangle \) et \(M_{23}^2 = \left\langle {\left( {v_2 - v_3 } \right)i_2 } \right\rangle \)
Remarque : Les indications fournies par \(M_{23}^2 \) sont positives ou négatives selon l'angle \(\widehat{\vec U_{23} ,\vec I_2 }\)
Quelque soit le montage (équilibré ou non, sinusoïdal ou non) s’il n’y a pas de fil neutre:
\(M_{13}^1 + M_{23}^2 = \left\langle {\left( {v_1 - v_3 } \right)i_1 } \right\rangle + \left\langle { \left( {v_2 - v_3 } \right)i_2 } \right\rangle = \left\langle {v_1 i_1 - v_3 i_1 + v_2 i_2 - v_3 i_2 } \right\rangle \)
donc
\(M_{13}^1 + M_{23}^2 = \left\langle {v_1 i_1 + v_2 i_2 + v_3 \left( { - i_1 - i_2 } \right)} \right\rangle \)
et comme il n’y a pas de fil neutre alors \( - i_1 - i_2 = i_3 \)
donc
| \(M_{13}^1 + M_{23}^2 = \left\langle {v_1 i_1 + v_2 i_2 + v_3 i_3 } \right\rangle = P\) |
\( \begin{gathered} P = \vec V_{1N} \cdot \vec I_1 + \vec V_{2N} \cdot \vec I_2 + \vec V_{3N} \cdot \vec I_3 \hfill \\ P = \vec V_{1N} \cdot \vec I_1 + \vec V_{2N} \cdot \vec I_2 + \vec V_{3N} \cdot \left( { - \vec I_2 - \vec I_1 } \right) \hfill \\ P = \left( {\vec V_{1N} - \vec V_{3N} } \right) \cdot \vec I_1 + \left( {\vec V_{2N} - \vec V_{3N} } \right) \cdot \vec I_2 \hfill \\ P = \vec U_{13} \cdot \vec I_1 + \vec U_{23} \cdot \vec I_2 = M_{13}^1 + M_{23}^2 \hfill \\ \end{gathered} \)
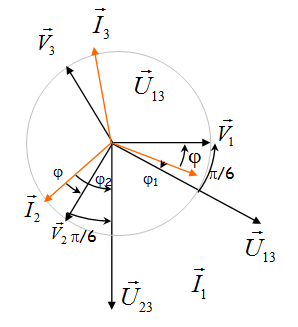
Pour la puissance réactive (charge triphasée équilibrée)
Le wattmètre W1 mesure \(M_{13}^1 = \left\langle {\left( {v_1 - v_3 } \right)i_1 } \right\rangle = U_{13} I_1 \cos \left( {\widehat{\vec U_{13} ,\vec I_1 }} \right) = U_{13} I_1 \cos \left( {\frac{\pi }{6} - \varphi } \right)\)
Le wattmètre W2 mesure \(M_{23}^2 = \left\langle {\left( {v_2 - v_3 } \right)i_2 } \right\rangle = U_{23} I_2 \cos \left( {\widehat{\vec U_{23} ,\vec I_2 }} \right) = U_{23} I_2 \cos \left( {\frac{\pi }{6} + \varphi } \right)\)
\(M_{13}^1 = U_{13} I_1 \left( {\cos \varphi \times \cos \left( {\frac{\pi }{6}} \right) + \sin \varphi \times \sin \left( {\frac{\pi }{6}} \right)} \right)\)
\(M_{23}^2 = U_{23} I_2 \left( {\cos \varphi \times \cos \left( {\frac{\pi }{6}} \right) - \sin \varphi \times \sin \left( {\frac{\pi }{6}} \right)} \right)\)
\( M_{13}^1 - M_{23}^2 = 2UI\sin \varphi \times \sin \left( {\frac{\pi }{6}} \right) = UI\sin \varphi \)
donc
| \( Q = \sqrt 3 \left( {M_{13}^1 - M_{23}^2 } \right) \) |





