Principe
Schéma
Les rôles de générateur et de récepteur sont inversés entre la source de tension et la source de courant par rapport au hacheur série (abaisseur)
- Le générateur a la nature d'une source de courant continu constant d'amplitude i ; il est unidirectionnel en tension.
- Le récepteur a la nature d'une source de tension unidirectionnelle en courant et sa structure est telle que la tension à ses bornes peut être considérée comme constante et d'amplitude E (cette condition est généralement assurée par un condensateur en parallèle de valeur élevée).
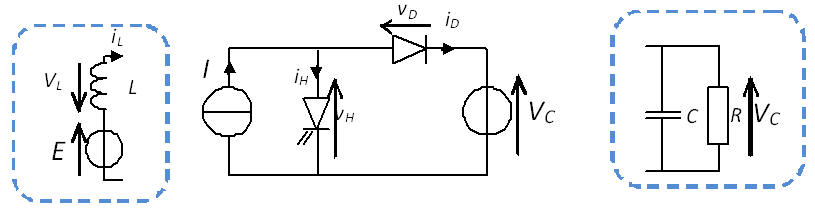
Structure de base et nature des charges et sources
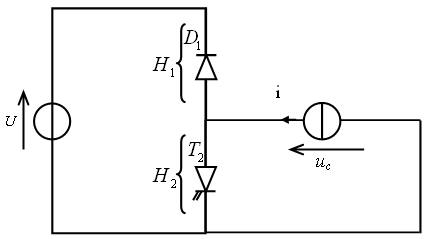
Principe de fonctionnement
Le hacheur parallèle permet d'élever la valeur d'une source de tension E. La source de tension est d'abord transformée en source de courant par ajout d'une inductance de lissage.
- La première phase de fonctionnement (H fermé) permet de stocker de l'énergie dans la bobine, pendant ce temps la tension est maintenue constante dans la charge grâce au condensateur.
- La seconde phase de fonctionnement décharge la bobine en série avec la source de tension dans la charge lui offrant ainsi une tension supérieure à E.
Fonctionnement en régime permanent : Conduction ininterrompue.
- H fermé : \( 0 <t < \alpha T \) :
- H ouvert : \( \alpha T <t < T \) :
Récapitulatif des courbes
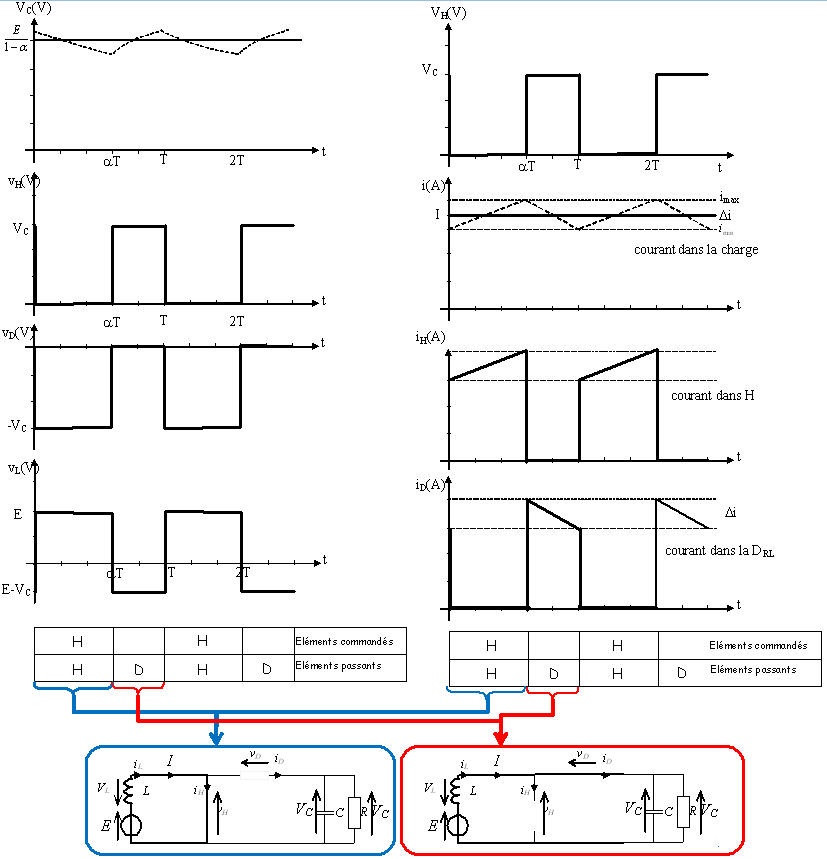
Relations sur les valeurs moyennes
Valeur moyenne de la tension
La tension moyenne aux bornes de la bobine parcourue par un courant périodique est nulle : \( \left\langle {{v_L}} \right\rangle = 0 \).
Pour retrouver la relation donnant la valeur de \( V_C \) on supposera la tension \( V_C \) maintenue constante (à l’aide d’un condensateur par exemple).
Ainsi , la valeur moyenne de \( v_D \) est \( \left\langle {{v_D}} \right\rangle = - \alpha {V_C} \).
Par ailleurs la valeur moyenne de \( v_H \) est \( \left\langle {{v_H}} \right\rangle = \alpha {V_C} \) .
La loi des mailles donne :
| \( {V_C} = \frac{E}{{\left( {1 - \alpha } \right)}} \) |
Où \( \alpha \) compris entre 0 et 1 la tension de sortie est toujours supérieure à Ve, le montage est élévateur de tension (survolteur)
- Il faut limiter la valeur de \( \alpha \) car s’il tend vers 1, VC tend vers l’infini ce qui aurait pour conséquence de claquer le condensateur.
- Même si la tension peut être augmentée, le courant disponible descend d'autant, la puissance de la source reste toujours limitée
Valeur moyenne du courant:
Pour les courants, à la lecture des courbes il vient immédiatement.
\( \left\langle I \right\rangle = \frac{{{I_{\max }} + {I_{\min }}}}{2} \approx I \)
\( \left\langle {{I_H}} \right\rangle = \alpha I \) et \( {I_H} = \sqrt \alpha I \)
\( \left\langle {{I_D}} \right\rangle = \left( {1 - \alpha } \right)I \) et \( {I_D} = \sqrt {1 - \alpha } I \)
Donc
\( I = \frac{{\left\langle {{I_D}} \right\rangle }}{{\left( {1 - \alpha } \right)}} \)
\( \left\langle {{I_H}} \right\rangle = \alpha I = \frac{{\alpha \left\langle {{I_D}} \right\rangle }}{{\left( {1 - \alpha } \right)}} \)
\( {I_H} = \sqrt \alpha I = \frac{{\sqrt \alpha \left\langle {{I_D}} \right\rangle }}{{\left( {1 - \alpha } \right)}} \)





