Principe :
Un Hacheur série associe une source de tension liée par intermittences à un récepteur de courant.
Schéma :
Le schéma de principe suivant transcrit les organes essentiels:
|  Schéma de principe |
| Le schéma suivant revient au même que le schéma précédent mais permettra d'insérer plus facilement d'autres cellules de commutation de façon à accéder aux autres quadrants de pilotage des hacheurs. | 
|
Séquences de conduction :
On manœuvre H de manière périodique donc les séquences de fonctionnement sont les suivantes
| 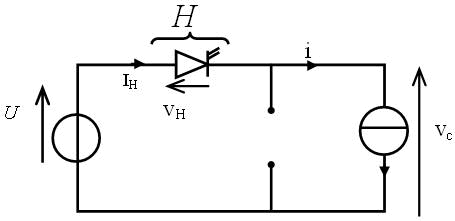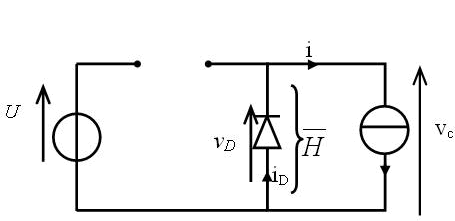 Séquences de fonctionnement |
Charges réceptrices de courant :
| Une charge réceptrice de courant est telle que le courant la traversant pourra être considéré comme constant.
Cet état de fait est assuré en général par un lissage du courant obtenu par la mise en série d'une inductance de lissage | 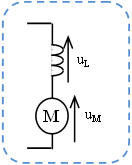 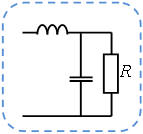
|
Rapport cyclique
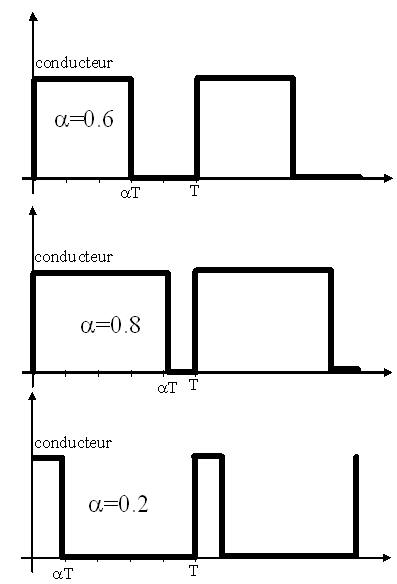
| Le rapport cyclique d'un interrupteur exprime le rapport du temps pendant lequel il est conducteur sur la période à laquelle on retrouve cette conduction.
Ce rapport \( \alpha \) est donc un nombre sans dimension compris entre 0 et 1. La période et le temps de conduction seront exprimés dans la même unité de temps.
| 
|

Tension de la charge
Courbes
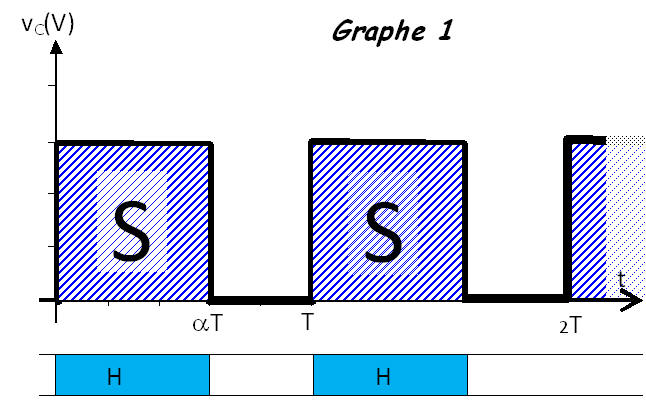
| 
Séquences de fonctionnement |
En manœuvrant H , on donne à v les valeurs alternées 0 et U. On fait varier la tension moyenne \( v_{c moy} \).
Valeur moyenne
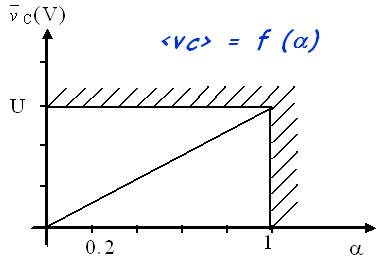
La valeur moyenne peut être calculée soit à l’aide d’une intégrale soit dans les cas simples en utilisant les formules de géométrie.
\( \left\langle {{v_C}} \right\rangle = \frac{1}{T}\int\limits_0^T v (t).dt = \frac{1}{T}\int\limits_0^{\alpha T} U .dt = \frac{S}{T} = \frac{{U \cdot \alpha \cdot T}}{T} = \alpha \cdot U \)
| \( \left\langle {{v_C}} \right\rangle = \overline {{v_C}} = \alpha U \) |
En réglant le rapport cyclique \( \alpha \) du hacheur, on règle la tension moyenne aux bornes de la charge alimentée par le hacheur
Valeur efficace de la tension de la charge
Comme \( V_c \) est la racine de la valeur moyenne de \( v_c^2(t) \) on obtient: \( {V_c^2} = \frac{{\alpha T \cdot {U^2}}}{T} \) donc
| \( {V_C} = \sqrt \alpha \cdot U \) |
Tension aux bornes de l'interrupteur
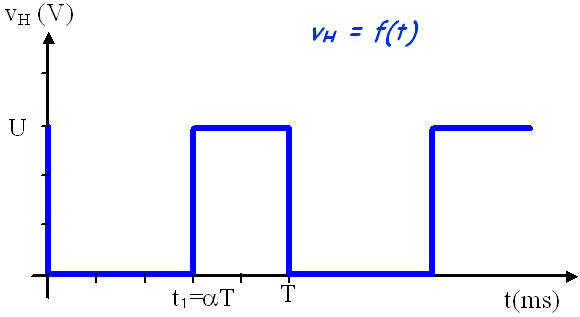
Fonctionnement sur charge inductive E,R,L ou R,L .
Conduction ininterrompue
La charge est constituée par exemple d'un petit moteur et d'une bobine suffisamment grande pour que le courant ne s'annule jamais.
La charge étant inductive une diode de roue libre D est nécessaire pour permettre l'écoulement de l'énergie sans apparition de surtension préjudiciable pour H.
Le critère important pour que les portions du signal courant soient des droites est que la constante de temps soit très supérieure à la période de hachage soit : \( \tau = \frac{L}{R} >> T \)
Récapitulatif des courbes

Remarque : Si R n’est pas négligeable, la forme des courants est différente.On retrouve alors des arcs d’exponentielle propres à l'établissement du courant dans une charge RL.
Analyse du courant
Équations du courant
Lors de chaque phase, la loi des mailles donne :
- H fermé de 0 à \( \alpha T \): \( {v_C} = U = E + Ri + L\frac{{di}}{{dt}} \) donne l’équation différentielle \( i + \frac{L}{R}\frac{{di}}{{dt}} = \frac{{U - E}}{R} \)
- H ouvertde \( \alpha T \) à T: \( {v_C} = 0 = E + Ri + L\frac{{di}}{{dt}} \) donne l’équation différentielle \( i + \frac{L}{R}\frac{{di}}{{dt}} = \frac{{ - E}}{R} \)
La résolution de ces équations différentielles donnerait lieu à des réponses exponentielles propres aux régimes transitoires du premier ordre.
Si la constante de temps du système \( \tau = \frac{L}{R} \gg T \) la période de hachage alors les équations de l’évolution du courant dans la charge sont des portions de droites.
- Lorsque H fermé de 0 à \( \alpha T \): \( {v_C} = U = E + L\frac{{di}}{{dt}} \) \( \Rightarrow \frac{{di}}{{dt}} = \frac{{U - E}}{L} \) donc l'équation de l'évolution du courant lors de la phase de charge est: \( \Rightarrow {i_1}(t) = \frac{{U - E}}{L} \cdot t + i_{min} \)
- Lorsque H ouvertde \( \alpha T \) à T: \( {v_C} = 0 = E + L\frac{{di}}{{dt}} \) \( \Rightarrow \frac{{di}}{{dt}} = \frac{-E}{L} \) donc l'équation de l'évolution du courant lors de la phase de décharge est: \( \Rightarrow {i_2}(t) = \frac{-E}{L} \cdot (t- \alpha T) + i_{max} \)
Ondulation du courant
Pour trouver l'ondulation du courant, il suffit d'écrire dans l'une des deux équations ci dessus, la valeur atteinte en fin de phase de conduction.
Donc \( {i_1}(\alpha T) = i_{max} = \frac{{U - E}}{L} \cdot \alpha T + i_{min} \)
Donc l'ondulation du courant \( \Delta i = i_{max} - i_{min} \)
Donc \( \Delta i = \frac{{U - E}}{L} \cdot \alpha T \)
Donc en remplaçant \( T=\frac{1}{f} \) et \( E = \alpha U \)
Donc \( \Delta i = \frac{{U - E}}{{Lf}} \cdot \alpha = \frac{{U - \alpha U}}{{Lf}} \cdot \alpha = U\frac{{\left( {1 - \alpha } \right) \cdot \alpha }}{{Lf}} \)
L'expression de l'ondulation du courant est donc
| \( \Delta i = U\frac{{\left( {1 - \alpha } \right) \cdot \alpha }}{{Lf}} \) |
Maximum d'ondulation du courant
L'expression \( \Delta i = U\frac{{\left( {1 - \alpha } \right) \cdot \alpha }}{{Lf}} \) admet un maximum lorsque sa dérivée s’annule.
\( \frac{{d\left( {\Delta i} \right)}}{{d\alpha }} = \frac{U}{{Lf}}\frac{{d\left( {\left( {1 - \alpha } \right) \cdot \alpha } \right)}}{{d\alpha }} = \frac{U}{{Lf}}\left( {1 - 2\alpha } \right) = 0 \)
Donc lorsque \( 1 - 2\alpha =0 \) soit lorsque \( \alpha =\frac{1}{2} \)
Alors l'ondulation est maximum et vaut \( \Delta {i_{\max }} = \frac{U}{{4Lf}} \)
Il apparait alors évident que pour diminuer l’ondulation, il faut
- augmenter f (action limitée par les durées de commutation des transistors)
- augmenter L(encombrement).
Valeurs moyennes des courants
La loi des mailles permet d’écrire: \( v = Ri + E + L\frac{di}{dt}\)
Donc la valeur moyenne de l'expression donne \( \bar v = R\bar i + E + \overline {L\frac{{di}}{{dt}}} \)
et comme
- la tension moyenne aux bornes d'une bobine parcourue par un courant périodique est nulle
- et \( \bar v = \alpha U \)
Donc le courant moyen
| \( \bar i = \frac{{\alpha U - E}}{R} \) |
Cette détermination du courant moyen peut être mise en parallèle de celle-ci :
| \( \bar i = \frac{i_{max}+i_{min}}{2} \) |
Et permettre ainsi de déterminer les valeurs des courants \( i_{max} \) et \( i_{min} \)
De la définition du courant moyen on peut aussi déduire facilement:
- le courant moyen dans la diode \( {\bar i_D} = (1 - \alpha )\bar i \)
- le courant moyen dans l’interrupteur \( {\bar i_H} = \alpha \bar i \)
Vidéos Animation:
| Study with Nour: 24. Hacheur série à débit non interrompu dans la bobine | DNI (24'24") |
| https://youtu.be/SUHppgzMdVM |
| Study with Nour: 25. Hacheur série à débit interrompu dans la bobine | DI |
| https://youtu.be/diMJxIC23UU |
| Study with Nour: 17. Exercice corrigé- hacheur série part1 (13'31") |
| https://youtu.be/Yy7l9gVJdh4 |
| Study with Nour: 18. Exercice corrigé - hacheur série part2 (15'13") |
| https://youtu.be/zxgBsPm6kLU |
| Denis Raynaud: hacheur série principe variateur MCC (6'07") |
| https://youtu.be/zWHNM9dsuos |
| Denis Raynaud: conduction continue et discontinue hacheur série (6'52") |
| https://youtu.be/3SMJbfieNno |

|
QCM en ligne
- http://fabrice.sincere.free.fr/qcm/qcm.php?nom=qcm_hacheur
- http://fisik.free.fr/?choix=qcm&typeqcm=hacheur&qnum=60






