A faire
- Puissances échangées
- Liens vers fichiers PSIM
Séquence des commandes des interrupteurs:
- De 0 à T/2 : \( K_1 \) est commandé
- De T/2 à T : \( K_2 \) est commandé
La diode placée en antiparalèlle permet le passage du courant dans les 2 sens.
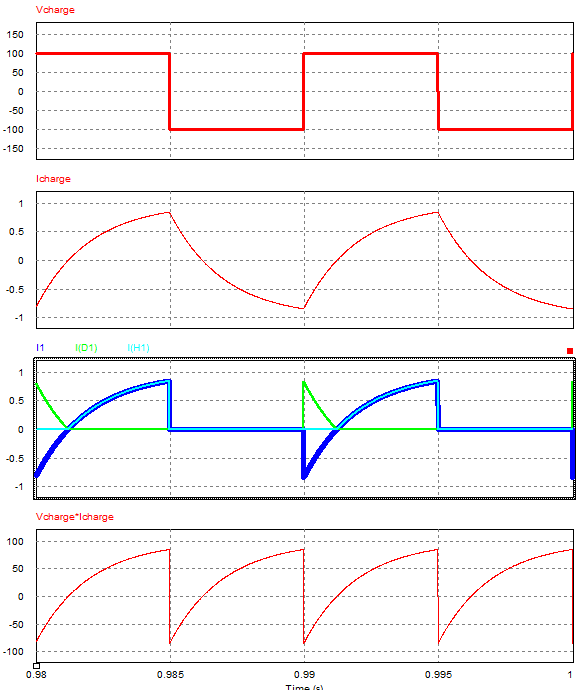
Étude de la tension \( u_c(t) \) :
- De 0 à T/2 : \( u_c(t) = E \)
- De T/2 à T : \( u_c(t) = -E \)
La valeur moyenne de \( u_c(t) \) : \( \left\langle {{u_c}(t)} \right\rangle = 0 \)
La valeur efficace de \( u_c(t) \) : \( {U_c} = E \)
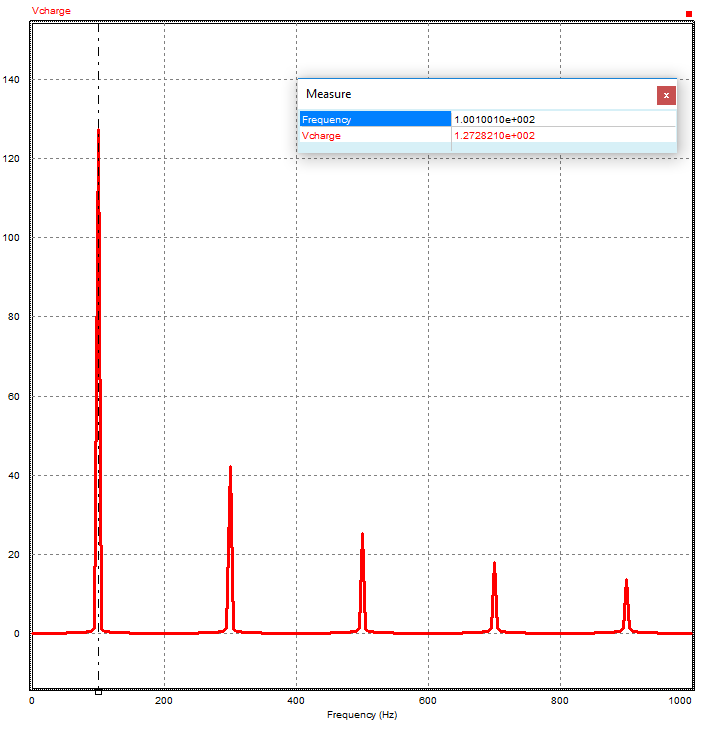
Décomposition spectrale de \( u_c(t) \) :
La tension \( u_c(t) \) est une fonction créneau impaire , sa décomposition ne contient que des termes en sinus et ne présente que des harmoniques pairs :
\( {u_c}\left( t \right) = \sum\limits_{k = 0}^\infty {\frac{{4E}}{{\left( {2k + 1} \right)\pi }}\sin \left( {2k + 1} \right)\omega t} \)
Etude des courants:
Exemples:
Le courant dépend de la nature de la charge.
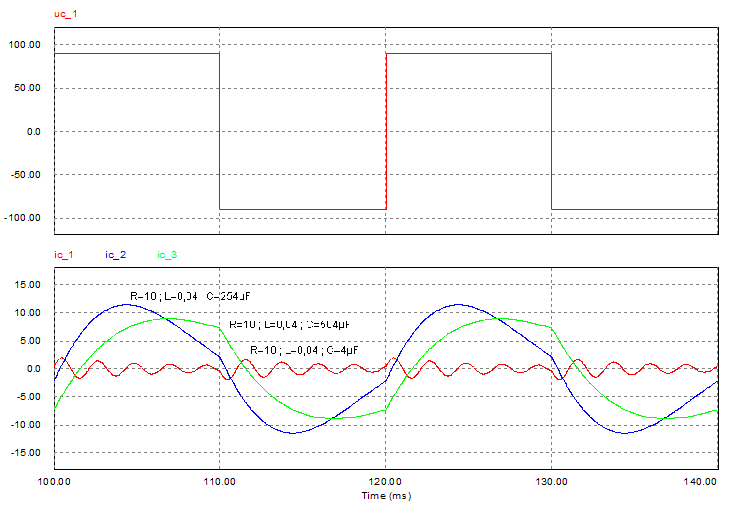
| Exemple de courants pour diverses valeurs de l’inductance d’une charge RL | Exemple de courants pour diverses valeurs de l’inductance d’une charge RLC |

| 
|
Constatations:
Comme le courant n’es pas sinusoïdal, il est riche en harmoniques (de même fréquences que la tension) qui
- génèrent des couples pulsatoires néfastes sur les machines tournantes
- génèrent des parasites radioélectriques pouvant perturber des signaux de commande.
Méthode d’étude:
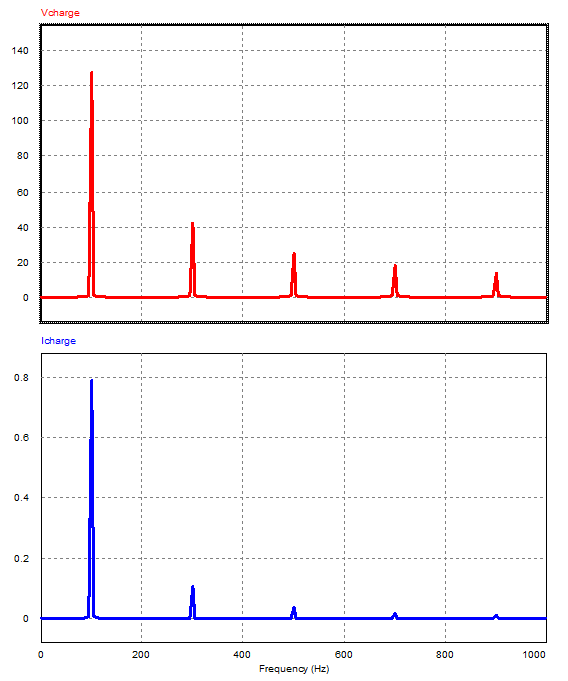
On peut associer une impédance complexe \( \underline{Z}_{n\omega} \) à chaque harmonique de rang n de la tension.
D’après le théorème de superposition, le courant i(t) ne contient que les harmoniques de la tension u(t) Ainsi pour chaque harmonique :
\( i\left( t \right) = \sum\limits_{k = 0}^\infty {\frac{{4E}}{{\left( {2k + 1} \right)\pi \left| {{{\underline{Z}}_{\left( {2k + 1} \right)\omega }}} \right|}}\sin \left[ {\left( {2k + 1} \right)\omega t - \arg \left( {{{\underline{Z}}_{\left( {2k + 1} \right)\omega }}} \right)} \right]} \)
On observe que le courant voit son spectre s’amoindrir nettement plus vite que celui de la tension. En effet l’impédance de la charge va grandissant avec la fréquence, réduisant ainsi le courant.
Puissances transférées :
La puissance instantanée fournie par à la charge est donc \( p_{charge} = v_{charge} \times {i_{charge}} \)
La charge passe par des phases de consommation et des phases de restitution.
La puissance active consommée par la charge est la puissance moyenne instantanée: \( P_{charge}= \left\langle {{p_{charge}}} \right\rangle = \left\langle {v_{charge} \times {i_{charge}}} \right\rangle \)