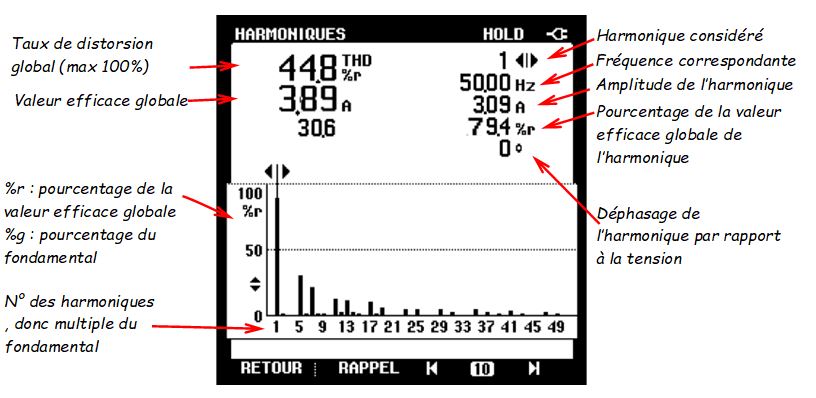
Taux de distorsion harmonique
On quantifie la déformation d’un signal par rapport à une sinusoïde parfaite par le taux de distorsion harmonique.
Cette grandeur fait le rapport de la valeur efficace des harmoniques sur le fondamental (THD) la valeur efficace du signal (TGD):
La valeur efficace des harmoniques (les sinusoïdes autres que le fondamental) est \( \sqrt {\sum\limits_{n = 2}^\infty {I_n^2} } = \sqrt {{I^2} - I_1^2 - I_0^2} \)
| \( THD = \frac{{\sqrt {\sum\limits_{n = 2}^\infty {I_n^2} } }}{I_1} = \frac{{\sqrt {{I^2} - I_1^2 - I_0^2} }}{I_1} \) |
THD
Le THD divise donc la valeur efficace des harmoniques sur le fondamental: \( I_1 \) et donc \( THD = \frac{{\sqrt {\sum\limits_{n = 2}^\infty {I_n^2} } }}{{{I_1}}} = \frac{{\sqrt {{I^2} - I_1^2 - I_0^2} }}{{{I_1}}} \)
TGD
Le TGD divise donc la valeur efficace des harmoniques sur la valeur efficace du signal total: \( I \) et on l'appelle plutôt Taux Global de Distorsion \( TGD = \frac{{\sqrt {\sum\limits_{n = 2}^\infty {I_n^2} } }}{{{I_1}}} = \frac{\sqrt {{I^2} - I_1^2 - I_0^2} }{I} \)
Taux Individuel de l’Harmonique de rang h
Le taux individuel permet de quantifier l'importance d'un harmonique
\( S_h = \frac{I_h}{I_1}\)
\( I_h \) représente la composante harmonique de rang \( h \), \( I_1 \) représente la composante fondamentale
Relations avec le THD
La puissance déformante étant définie par \(D = {V_1} \times \sqrt {\sum\limits_{n = 2}^\infty {I_n^2} } \)
La puissance déformante est liée au Taux de Distorsion Harmonique par \( THD = \frac{D}{{{V_1}{I_1}}} = \frac{D}{{\sqrt {{P^2} + {Q^2}} }} \)

Mesure