Wiki du BTS Electrotechnique - SA

Vidéo mise en avant

Comment les résistances fonctionnent ? 15’09’’ Mentalité Ingénieur

Description

Une résistance ou résistor est un dipôle ne laissant pas parfaitement passer le courant, les électrons subissent des chocs sur les atomes du matériaux et l'échauffent.

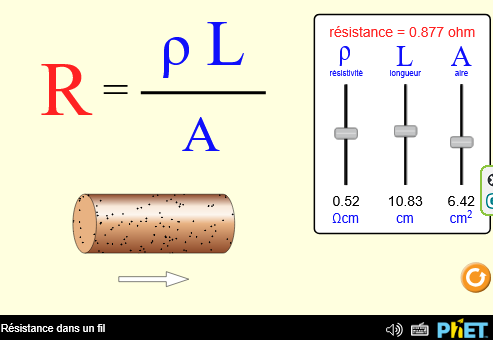
Chaque matériau présente une résistivité \( \rho \) qui est la capacité d'un matériau à empêcher la circulation des charges électriques, et donc, du courant.
Plus la distance parcourue \( \ell \) dans le matériau est grande, plus les chocs seront importants et la résistance augmente donc.
Si la section (surface par laquelle passe le courant) est plus importante, les électrons auront plus de place pour passer, la résistance diminue.

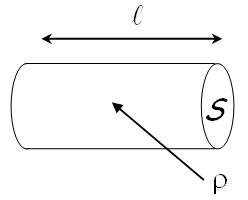
Ces observations permettent d'établir la valeur de la résistance d'un matériau connaissant ses caractéristiques techniques

\(R = \rho \times \frac{\ell}{S}\)

avec

\( R \) la résistance du composant en Ohm : \( \Omega \)
\( \rho \) la résistivité du matériau en \( \Omega \cdot m \)
\( \ell \) la résistance du composant en \( m \)
\( S \) la longueur du fil considéré en \( m^2 \)

Visualisez la résistivité dans cette animation!!!

Quelques différents types de résistances.

Que se passe-t-il dans une résistance?

Les électrons libres porteurs du courant se choquent à la matière, l'échauffent, l'énergie cinétique de ces électrons part donc en chaleur.

C'est l'effet Joules

L'échauffement du à l'effet Joules dépend du courant passant dans la résistance, la puissance perdue dans un conducteur dépend de sa résistance \( R \) et du courant qui le traverse: \( p=R \times i^2 \)

Relation liant tension et courant dans une résistance: loi d'Ohm

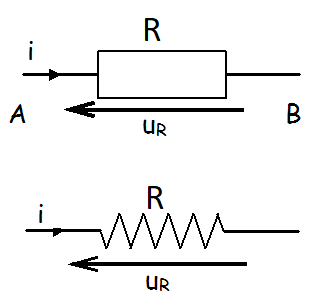
Symboles

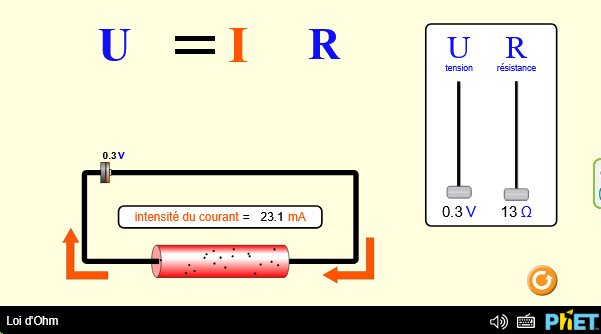
Si une résistance est alimentée par une tension \( u \) ou parcourue par un courant \( i \), alors il existe une relation liant les courant dans la résistance et la tension à ses bornes. La relation liant la tension au courant est

\( u=R \times i \)

avec

\( R \) la résistance du composant en Ohm \( \Omega \)
\( u \) la tension aux bornes du dipôle en Volts \( V \)
\( i \) l'intensité du courant en Ampères\( A \)

Visualisez la loi d'Ohm dans cette animation!!!

Le courant et la tension étant toujours proportionnels, la forme de la tension et la forme du courant sont toujours identiques:

si la tension est une sinusoïde, le courant le sera aussi (et sans déphasage)
si la tension est en dents de scie, le courant le sera aussi
si la tension est en créneaux, le courant le sera aussi

La caractéristique \( u \) en fonction de \( i \) est donc une droite de pente égale à R.

Associations de résistances

résistances en série:

La résistance équivalente à des résistances en série est telle que :

\( R_{eq}=R_1+R_2 \)

Dans plusieurs dipôles en série, le courant est commun à tous les dipôles, la loi des mailles s'applique \( u=u_1+u_2 \)

La tension \( u=R_{eq} \times i \)
Les tensions \( u_1=R_1 \times i \) , \( u_2=R_2 \times i \)
en regroupant tout dans la loi des mailles
en factorisant par i
puis en simplifiant par i

on retrouve \( R_{eq}=R_1+R_2 \)

Résistances en parallèle:

La résistance équivalente à des résistances en parallèle est telle que :

\( \frac{1}{R_{eq}}=\frac{1}{R_1}+\frac{1}{R_2} \).

Si l'on a des résistances en parallèles, le courant va se répartir sur les résistances, et la résistance globale est donc plus faible. La conductance équivalente \( G_{eq}=\frac{1}{R_{eq}} \) est la somme des conductances de chaque dipôle.

Dans plusieurs dipôles en parallèle, la loi des nœuds s'applique \( i=i_1+i_2+i_3 \)

Le courant \( i=\frac{u}{R_{eq}} \)
Les courants \( i_1=\frac{u}{R_1} \) , \( i_2=\frac{u}{R_2} \) , \( i_3=\frac{u}{R_3} \)
en regroupant tout dans la loi des nœuds
en factorisant par u
puis en simplifiant par u

on retrouve \( \frac{1}{R_{eq}}=\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3} \)

Si l'on n'a que deux résistances alors \( R_{eq}=\frac{R_1 \times R_2}{R_1 + R_2} \)

Mais si l'on en a plus alors la seule généralité que l'on peut écrire est \( \frac{1}{R_{eq}}=\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3} \)

La résistance en sinusoïdal

Valeurs instantanées:

Soient \( i(t) = I \sqrt{2} sin (\omega t + \varphi_i) \)

et \( u(t) = U \sqrt{2} sin (\omega t + \varphi_u) \)

la loi d'Ohm impose que \( u(t) = R i(t)\)

Donc \( u(t) = RI \sqrt{2} sin (\omega t + \varphi_i) \)

Les valeurs efficace de chacun des signaux doivent être égales donc \( \Rightarrow U = R I \)

Les phases à l'origine aussi donc \( \varphi_u = \varphi_i \)

Construction de Fresnel:

courant et tension sont en phase

Impédance complexe:

\( \left| {\underline {{Z_R}} } \right| = \frac{{\left| {\underline U } \right|}}{{\left| {\underline I } \right|}} = \frac{{RI}}{I} = R \)

et \( \varphi_Z = 0 \)

soit

\( \underline{Z}_R = R \)

\( \underline{U} = R \times \underline{I} \)

Puissance active:

\( P_R = R \times I^2 = \frac{U^2}{R} \)

Puissance réactive:

\( Q_R = 0 \)

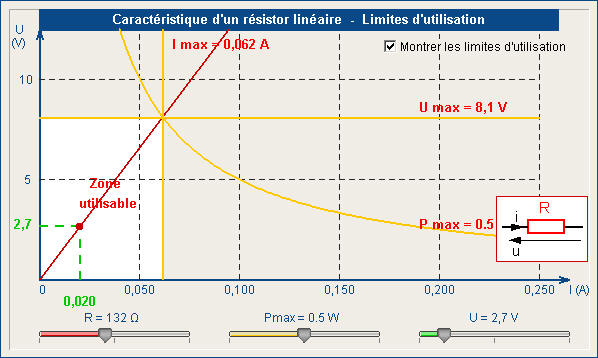
Courbes caractéristiques et limitations d'une résistance

Le constructeur prescrit \( P_{max} \) dont on déduit \( I_{max} \) et \( U_{max} \).

Cette puissance dissipée sous forme de chaleur est responsable de la destruction du composant

Quelques résistances en fonctions de leur puissance admissible.

Applet java sur la caractéristique d'une résistance, sa limitation en tension et courant

Caractéristiques d'une résistance

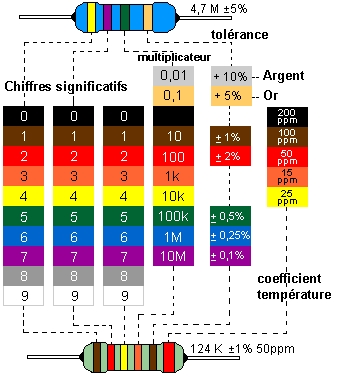
Ne (NOIR)	Manger (MARRON)	Rien (ROUGE)	Ou (ORANGE)	Jeûner (JAUNE)	Voila (VERT)	Bien (BLEU)	Votre (VIOLET)	Grande (GRIS)	Bêtise (BLANC)
0	1	2	3	4	5	6	7	8	9
\( 10^0=1 \)	\( 10^1=10 \)	\( 10^2=100 \)	\( 10^3=1k \)	\( 10^4=10k \)	\( 10^5=100k \)	\( 10^6=1M \)	\( 10^7=10M \)	\( 10^8=100M \)	\( 10^9=1G \)

Divers usages des résistances:

Les résistances de faibles puissances servent pour fixer des tensions, et des courants dans des montages d'électroniques, leur valeur est la caractéristique importante.
Les résistances de fortes puissances sont utilisées pour leurs pertes par effet joules comme moyen de chauffage. Sur ces résistances sera indiquée la puissance disponible sous telle tension d'utilisation
La valeur de la résistivité augmente avec la température, elles peuvent donc servir de capteur de température. On retrouve ce principe utilisé dans les PT100 et PT100 (résistances à fil de platine) , les CTN (résistance à coefficient de température négatif) et CTP (à coefficient de température positif).
l'éclairement peut aussi influer sur leur résistance, elles sont dans ce cas appelées photorésistances et permettent d'avoir une image électrique d'un éclairement.
une résistance soumise à une contrainte peut voir sa longueur et/ou sa section évoluer, modifiant par ce fait sa résistance. Les résistances exploitant ce phénomène sont appelées jauges de contrainte.