Précision et stabilité sont deux exigences contradictoires mais peut-on améliorer l’un sans trop détériorer l’autre ?
Des méthodes théoriques de calcul des paramètres permettent de déterminer précisément les valeurs de réglage. Elles nécessitent cependant la connaissance du modèle mathématique (circuit équivalent) du système à commander ! Leur efficacité dépend de la précision et de la robustesse du modèle. C’est pourquoi, dans l’industrie elles sont rarement utilisées, surtout pour la commande des processus complexes. Pour simplifier, on retiendra deux méthodes :
- en Boucle Ouverte (Broïda il est cependant rare que l’on puisse faire des essais en BO)
- en Boucle Fermée (Ziegler & Nichols ou méthode de l’ultime pompage).
Réglage industriel : modélisation, critères et réglage de Broïda
On applique un échelon à l’entrée du système non bouclé et on observe la réponse
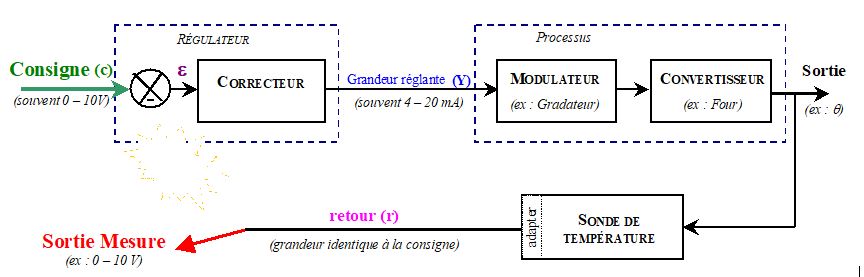
Lorsque la réponse à un échelon du système en boucle ouverte ne présente pas de rebond mais qu’il existe un retard entre l’échelon et la réponse, le modèle de Broïda peut être utilisé.
La fonction de transfert isomorphe est alors décrite de la façon suivante: \( H(p) = \frac{{K{e^{ - Tp}}}}{{1 + \tau p}} \)
Cette fonction de transfert fait apparaître une fonction du premier ordre de gain \( k \) est de constante de temps \( \tau \) couplée à une fonction retard de temps \( T \)
- Avec \( K \) le gain statique toujours défini comme \( K= \frac{\Delta{s}}{\Delta{e}} \)
- La constante de temps \( \tau \) est souvent prise égale à la pente au point d’inflexion, mais une méthode plus précise préconise de

Plus le retard est grand plus, le décalage dans le temps de la fonction est grand.
En fonction du rapport \( \frac{T}{\tau} \) divers correcteurs sont proposés :
| rapport \( \frac{T}{\tau} \) | Correcteur proposé |
|---|---|
| < 0,05 | TOR |
| Entre 0,05 et 0,1 | P |
| Entre 0,1 et 0,2 | PI |
| Entre 0,2 et 0,5 | PID |
| > 0,5 | Limite des PID, Chaines maillées... |
Le critère retenu par Broïda dans son mode de calcul des correcteurs est une marge de Gain de 6dB

Ziegler et Nichols
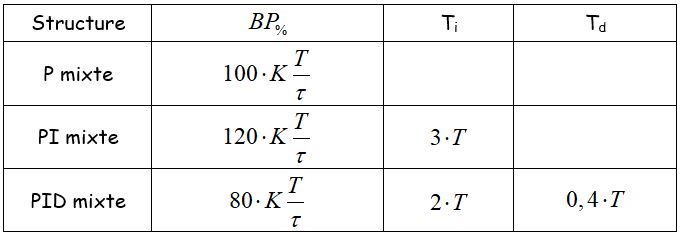
Ils proposent des choix de correcteurs plus durs (marge de stabilité plus faible) correspondant au critère de performance IAE ( reduction de l’intégrale d’erreur) plus adaptées aux servomécanismes. Chaque système est caractérisé par sa signature \( K\frac{T}{\tau } \).
Le point d’inflexion est est généralement obtenu à 20% du temps nécesaire à l’obtention de l’asymptote horizontale.
....
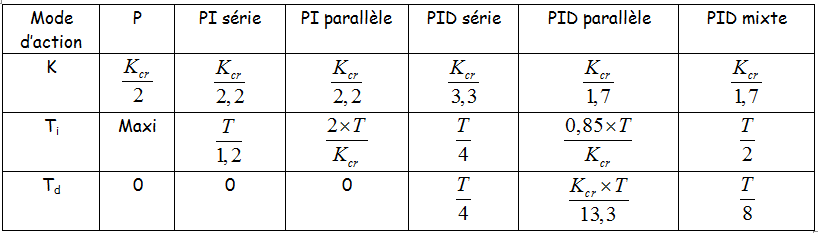
Réglage industriel par la méthode de Ziegler Nichols ou méthode de l’ultime pompage
Le but est de faire osciller le système pour connaître sa pulsation propre (ou fréquence propre) afin de pouvoir appliquer les réglages proposés dans le tableau suivant. Deux méthodes existent : l’ultime pompage (ci-dessous) et l'essai en TOR (ci-après).
- Configurer le régulateur en manuel puis attendre que le système soit complètement stabilisé,
- Afficher \( T_d = 0 \), intégrale minimale (afficher Ti maximal),
- Afficher un gain \( K=1 \) (\( BP=100\% \))
- Mettre la consigne égale à la mesure, et passer en automatique,
- Augmenter le gain (diminuer la bande proportionnelle) jusqu’à l ’apparition du pompage, fixer alors à cet instant le gain critique \( K_{cr} \) et la période des oscillations \( T_0 \).
- Afficher alors les paramètres du régulateur selon le tableau précédent.