Le radian
|
Le radian est défini comme le rapport la longueur de la corde \( \ell \) du cercle de rayon \( R \)
| 
| https://www.youtube.com/watch?v=9_XfAr0_Wfc
Clipédia (22'30") |
Cosinus
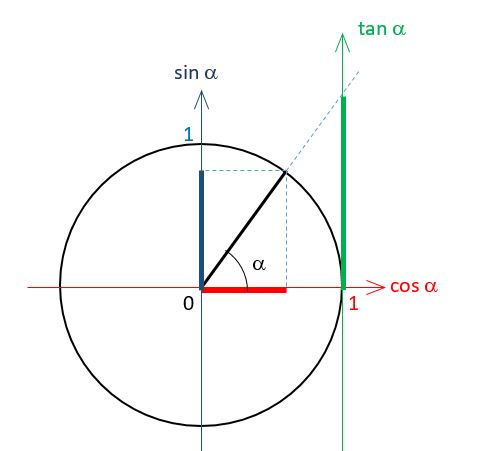
Le cosinus d'un angle \( \alpha \) correspond à la longueur de la projection sur l'horizontale d'un rayon de longueur 1 et incliné d'un angle de \( \alpha \) radians.
Sinus
Le sinus d'un angle \( \alpha \) correspond à la longueur de la projection sur la verticale d'un rayon de longueur 1 et incliné d'un angle de \( \alpha \) radians.
La loi des sinus (10'16") https://www.youtube.com/watch?v=mUIBgguuDw8
phet Colorado visualisation sinus trigo
Tangente
La tangente d'un angle \( \alpha \) correspond à la longueur du segment
- partant du point tangent à la verticale
- et qui se poursuit par la verticale jusqu'à la droite passant par le rayon incliné d'un angle de \( \alpha \) radians.
Relations de trigonométries
Relation fondamentale utilisée en électrotechnique
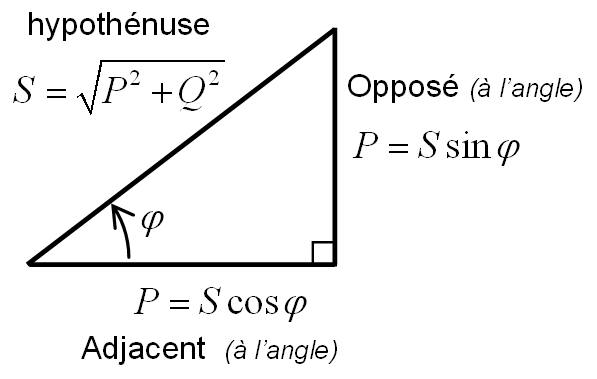
Les relations les plus importantes pour l'électrotechnicien sont celles présentes dans un triangle rectangle, qui lient chaque longueur, les angles et les sinus et cosinus de ces angles. Sur le triangle rectangle ci-dessous si on nomme:
- P le côté adjacent à l'angle \( \varphi \)
- Q le côté opposé à l'angle \( \varphi \)
- S l'hypothénuse
Alors les relations du triangle sont les suivantes
- le sinus de l'angle \( \varphi \) est tel que \( sin \varphi = \frac{coté opposé}{hypothénuse} \) soit \( sin \varphi = \frac{Q}{S} \)
- le cosinus de l'angle \( \varphi \) est tel que \( cos \varphi = \frac{coté adjacent}{hypothénuse} \) soit \( cos \varphi = \frac{P}{S} \)
- la tangente de l'angle \( \varphi \) est telle que \( tan \varphi = \frac{coté opposé}{adjacent} \) soit \( tan \varphi = \frac{Q}{P} \)
Ces trois dernières relations sont résumées par les mnémotechniques suivantes:
| \( SOHCAHTOA\) |
| ou \(\frac{CASOTO}{HHA} \) |
- et Pythagore nous donne une dernière relation \( {hypothénuse}^2 = {coté adjacent}^2 + {coté opposé}^2 \) soit \( S = \sqrt{P^2+Q^2} \)
Périodicité et valeurs particulières des fonctions trigonométriques
- \( cos^2 x + sin^2 x = 1 \)
- \( cos(x+2\pi) = cos x \)
- \( sin(x+2\pi) = sin x \)
| \( cos(-x) = cos x \) | \( cos(\pi+x) = -cos x \) | \( cos(\pi-x) = -cos x \) | \( cos(\frac{\pi}{2}-x) = sin x \) |
| \( sin(-x) = -sin x \) | \( sin(\pi+x) = sin x \) | \( sin(\pi-x) = sin x \) | \( sin(\frac{\pi}{2}-x) = cosx \) |
| x | 0 | \( \frac{\pi}{6} \) | \( \frac{\pi}{4} \) | \( \frac{\pi}{3} \) | \( \frac{\pi}{2} \) |
|---|---|---|---|---|---|
| cos x | 1 | \( \frac{\sqrt{3}}{2} \) | \( \frac{\sqrt{2}}{2} \) | \( \frac{1}{2} \) | \( 0 \) |
| sin x | 0 | \( \frac{1}{2} \) | \( \frac{\sqrt{2}}{2} \) | \( \frac{\sqrt{3}}{2} \) | 1 |
| tan x | 0 | \( \frac{1}{\sqrt{3}} \) | \( 1 \) | \( \sqrt{3} \) | \( \inf \) |
Relations d'addition, soustraction, multiplication des fonctions trigonométriques
- \( cos(a+b) = cos a \cdot cos b - sin a \cdot sin b \)
- \( sin(a+b) = sin a \cdot cos b + sin b \cdot cos a \)
- \( tan(a+b) =) = \frac{tan a +tan b}{1-tan a tan b} \)
- \( cos 2a = 2 cos^2 a - 1 \)
- \( cos 2a = 1 - 2 sin^2 a \)
- \( cos 2a = cos^2 a - sin^2 a \)
- \( sin 2a = 2 sin a \cdot cos a \)
- \( tan 2a = \frac{2 tan a}{1- tan^2 a} \)
- \( cos a \cdot cos b = \frac{1}{2}\left[ cos(a+b) + cos (a-b) \right] \)
- \( sin a \cdot sin b = \frac{1}{2}\left[ cos(a-b) - cos (a+b) \right] \)
- \( sin a \cdot cos b = \frac{1}{2}\left[ sin(a+b) + sin(a-b) \right] \)
- \( cos p + cos q = 2 cos \frac{p+q}{2} \cdot cos \frac{p-q}{2} \)
- \( sin p + sin q = 2 sin \frac{p+q}{2} \cdot cos \frac{p-q}{2} \)
Leçons de choses - partie 4 : formules de trigonométrie (9'44") https://www.youtube.com/watch?v=yTQxjJ73lgM





