Définition de la valeur efficace
L'intensité efficace I d'un courant variable i(t) prise sur un temps \( \Delta t \) est l'intensité du courant continu qui dissiperait par effet Joules dans une résistance la même énergie.
La valeur efficace est donc \( I = \sqrt{<i^2 (t)>} \)
En effet la puissance P dépensée dans une résistance est
- \( P = R \times i(t)^2 \) si le courant est variable
- \( P = R \times I^2 \) si le courant est continu
L'énergie W étant la moyenne des puissances consommées à chaque instant multiplié par le temps d'usage de ces puissances, on peut donc noter (la notation entre <> indique que c'est une valeur moyenne):
- \( W = R \times <i(t)^2> \times \Delta t \) si le courant est variable
- \( W = R \times <I^2> \times \Delta t \) si le courant est continu. Comme le courant est continu: \( <I^2>=I^2 \)
Comme dans la définition de la valeur efficace, les énergies doivent être équivalentes, on peut égaliser les deux équations.
\( W = R \times <i(t)^2> \times \Delta t= R \times I^2 \times \Delta t \)
Puis simplifier par R et \( \times \Delta t \)
Donc \( <i(t)^2> = I^2 \) soit \( I = \sqrt{<i^2 (t)>} \)
Le lien vers le fichier suivant permet de comparer l'éclairement et donc les pertes joules générés par d'un côté un signal continu et de l'autre un signal sinusoidal
Valeur efficace d'un signal sinusoïdal
Uniquement pour un signal sinusoïdal la valeur efficace d'une grandeur \( v(t)=V_{max} sin (\omega \times t) \) est notée V (en majuscule) et vaut \( V=\frac{V_{max}}{\sqrt{2}} \)
Mesure d'une valeur efficace
Elle se mesure avec
- Cas des appareils analogiques: On utilise des appareils ferromagnétiques (Symbole: \( \sum \) ou
 ) qui tendent à disparaître.
) qui tendent à disparaître.
- Cas des appareils numériques: On utilise des appareils « RMS ». (Parfois en position AC+DC). Attention certains appareils ne mesurent une valeur efficace que si la grandeur est sinusoïdale.
Rappels sur la mesure au multimètre
Méthode générale de détermination de la valeur efficace:
De part la définition de la valeur efficace d'une grandeur \( x(t) \) : \( X = \sqrt{<x^2 (t)>} \), la détermination de la valeur efficace amènera aux étapes suivantes:
- mettre le signal au carré
- trouver la valeur moyenne du signal déterminé précédemment
- prendre la racine du résultat
Remarque: On peut se souvenir de la définition de la valeur efficace grâce à son appellation anglo-saxonne : TRMS. TRMS étant l'acronyme de True Root Mean Square ( True: Vraie ,Root:Racine, Mean: Valeur Moyenne, Square: Carré)
Pour des cas simples:
Si la fonction dont on cherche la valeur efficace n'est constituée que de portions d'horizontales, la détermination peut se faire simplement graphiquement.
- le signal est mis au carré ( chaque portion droite reste droite et d'une valeur égale à son carré)
- la valeur moyenne du signal déterminé précédemment se résume à une succession de rectangles
- puis on prend la racine du résultat
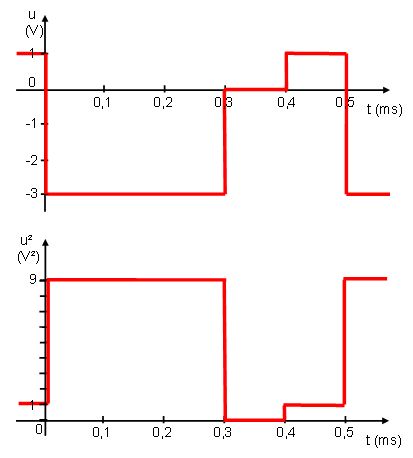
\( <u²>=\frac{Aire}{T}= \frac{ (9 \times 0.3) + (1 \times 0.1) }{0,5}= 5.6 V²\)
Donc la valeur efficace est de \( U=\sqrt{5.6}= 2.36 V\)
Pour des fonctions périodiques dont on connait la décomposition spectrale:
Si on a une fonction périodique \( x(t) \) de fréquence \( f_0 \), elle peut être décomposée en la somme
- d'une valeur moyenne
- d'une sinusoïde de fréquence égale à la fréquence du signal \( f_0 \)
- d'harmoniques de fréquences \( 2 \times f_0 , 3 \times f_0 , 4 \times f_0 ...\)
\( x(t) = \underbrace {\left\langle {x(t)} \right\rangle }_{valeur moyenne} + \underbrace {\sum\limits_{n = 1}^{ + \infty } {{{\hat X}_n}\cos (n{\omega _0}t + {\varphi _n})} }_{les harmoniques} \)
Le spectre est représenté de la façon suivante:
- en ordonnée sera représenté la valeur efficace de chaque sinusoïde
- l'abscisse indique la valeur de chaque fréquence
- on retrouve donc de gauche à droite, la valeur moyenne, le fondamental, les harmoniques.

Alors sa valeur efficace est la racine de la somme des carrés de ses harmoniques.
\( X = \sqrt { < {x^2}(t) > } = \sqrt {{{\left\langle {x(t)} \right\rangle }^2} + \sum\limits_{n = 1}^\infty {X_n^2} }= \sqrt {X_0^2+X_1^2+X_2^2+X_3^2...} \)
Quelques calculs classiques de valeurs moyennes et efficaces
- Exemples de calculs du site http://eleectrotechnique.fr : doc pdf
Valeur efficace de l'ondulation d'un signal:
Un signal dont la composante continue n'est pas nulle peut être séparé en deux parties: sa valeur moyenne et ses ondulations:
On peut écrire : \(x(t) = \left\langle {x(t)} \right\rangle + {x_{ond}}(t)\)
\( x_{ond} \) est la composante alternative de \( x(t) \) ou ondulation de \( x(t) \).
La valeur efficace de \( x_{ond} \) est \( X_{ond} \) telle que : \( X_{ond}^2 = X_1^2 + X_2^2 + ... + X_n^2 + ... \)
\( X_{ond} \) est appelée :
- valeur efficace de l'ondulation (AFNOR),
- valeur efficace RMS,
- valeur efficace AC (Alternating Current).
On remarque que : \( {X^2} = {\left\langle x \right\rangle ^2} + X_{ond}^2 \)
Cette relation est utile lorsqu'on utilise un appareil qui ne peut mesurer que \( \left\langle x \right\rangle \) et \( X_{ond} \) alors que l'on veut connaître la valeur efficace vraie.
On rencontre fréquemment des emplois abusifs du terme "efficace vrai", comme, par exemple, "efficace vrai pour l'alternatif seulement". Il est donc nécessaire d'être vigilant.






