Lorsque la réponse ne présente ni rebond ni retard , le modèle du premier ordre peut être utilisé.
Modèle simple mais très utilisé tant que le temps mort reste négligeable devant la constante de temps.
Equation différentielle : \( \tau \frac{{ds(t)}}{{dt}} + s(t) = k \cdot e(t) \)
Fonction de transfert isomorphe : \( H\left( p \right) = \frac{k}{{1 + \tau p}} \)
Réponse indicielle: \( s(t) = k \left( 1 - e^{ - \frac{t}{tau}} \right) \)
- le gain statique k est mesuré comme précédemment
- la constante de temps \( \tau \) est mesurée lorsque le système atteint 63% de la variation totale de la sortie.
- Comme la courbe atteint 95 % du maximum au bout d'un temps égal à 3 fois la constante de de temps alors le temps de réponse à 5% \( t_{r5\%} = 3 \times \tau \)
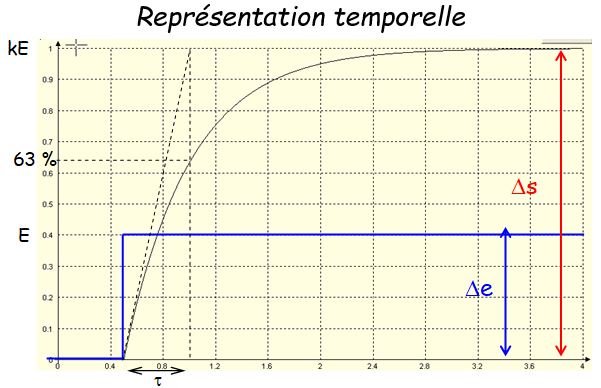
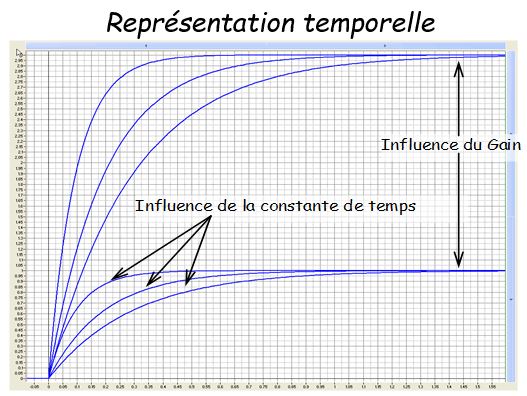
Influence de la constante de temps et du gain

Diagramme de Nyquist
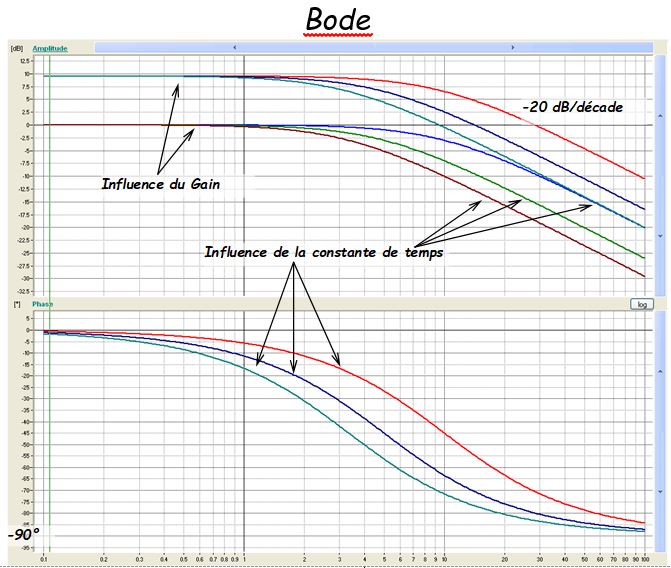
Diagramme de Nyquist
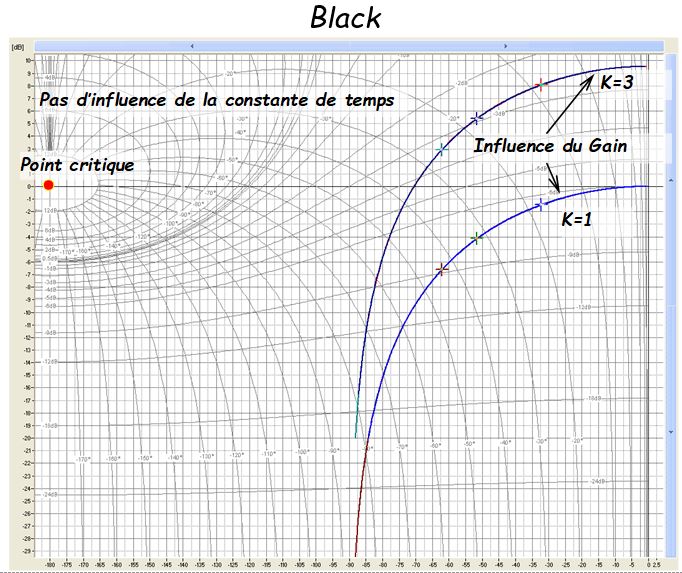
Diagramme de Black





