Lorsque la réponse présente un rebond, le modèle du deuxième ordre peut être utilisé.
Equation différentielle du système est de la forme : \( \frac{{{d^2}y}}{{d{t^2}}} + 2m{\omega _0}\frac{{dy}}{{dt}} + {\omega _0}^2y = g(t) \)
qui fait apparaitre :
- un gain statique k
- une pulsation propre \( \omega_0 \)
- un coefficient d'amortissement \( m \)
Fonction de transfert isomorphe : \( H\left( p \right) = k\frac{1}{{1 + \frac{{2mp}}{{{\omega _0}}} + \frac{{{p^2}}}{{\omega _0^2}}}} \)
Réponse indicielle : \( s(t) = k\left[ {1 - {e^{ - m{\omega _0}t}}\left( {\cos \omega t + \frac{{m{\omega _0}}}{\omega }\sin \omega t} \right)} \right] \) et ressemble donc à ceci
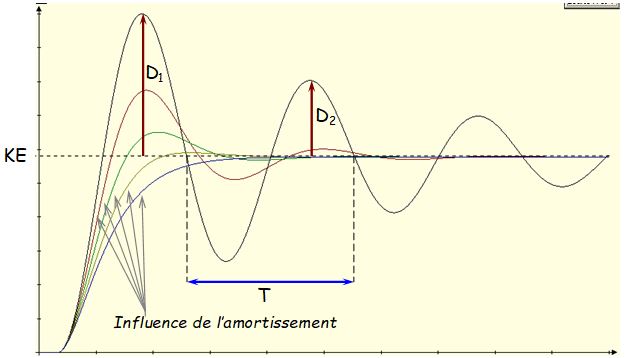
On peut déterminer:
- la période des oscillations et donc la pulsation d'oscillation \( \omega \) qui dans la réponse indicielle apparait liée à la pulsation propre du système \( \omega_0 \) par la relation \( {\omega _0} = \frac{{2\pi }}{{T\sqrt {1 - {m^2}} }} \) et \( \omega = \frac{{2\pi }}{T} \)
- la décroissance de ces oscillations est décrite par la valeur des dépassements \( D_1 \) , \( D_2 \) et ainsi de suite exprimés en pourcentage de la valeur finale.
D'après l'analyse de la réponse indicielle il s'avère que les dépassements dont tels que \( \frac{{{D_2}}}{{{D_1}}} = {e^{ - \frac{{2m\pi }}{{\sqrt {1 - {m^2}} }}}} \)
- le temps \( t_{r5\%} \) au bout duquel la réponse est comprise entre 95% et 105% de sa valeur stabilisée:
- On notera que le \( tr \) est mini si \( m=0,7 \) : \( {t_{r5\% \min }} = 0,44\frac{{2\pi }}{{{\omega _0}}} \)
- Si \( m << 1 \) alors \( \frac{{{t_{r5\% \min }}}}{{\frac{{2\pi }}{{{\omega _0}}}}} = \frac{3}{{2\pi m}} \Rightarrow {t_{r5\% \min }} = \frac{3}{{m{\omega _0}}} \)
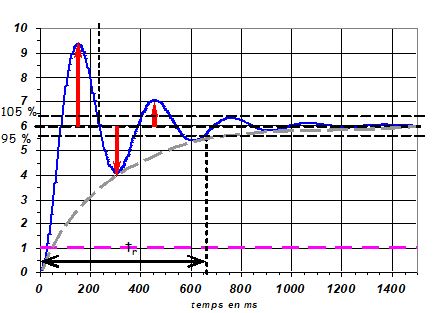
Connaissant la courbe de la réponse, la détermination de \( t_{r5\%} \) et de la pseudo pulsation \( \omega \) sont aisées à déterminer. Pour caractériser mathématiquement le système il faut réussir à déterminer le coefficient d'amortissement.
Pour cela une abaque est utilisée:
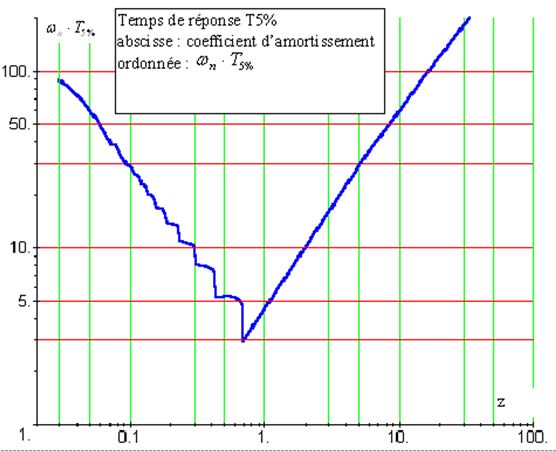
Pour connaitre l'amplitude et le nombre de dépassements, l'abaque suivante sera utilisée:
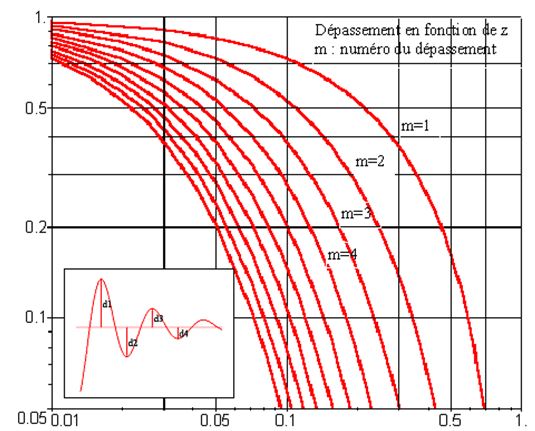
Les graphiques suivants montrent l'influence du coefficient d'amortissement.
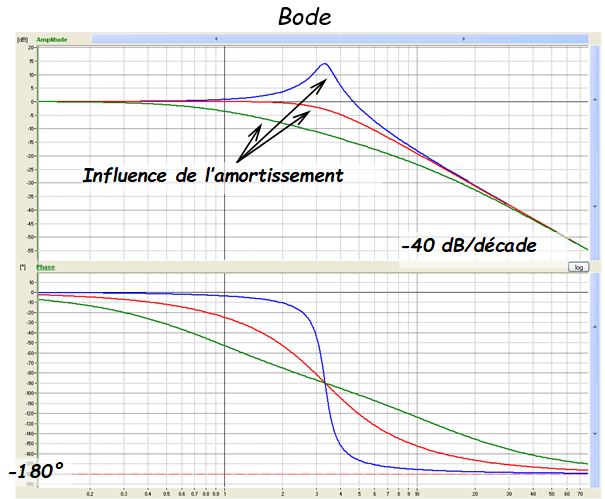
Diagramme de Bode
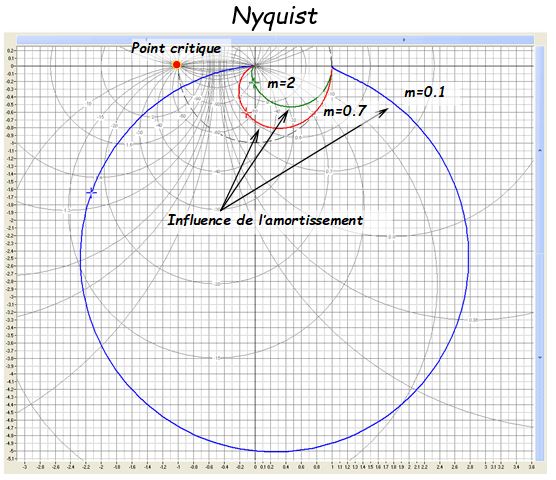
Diagramme de Nyquist
Diagramme de Black
