Critères graphiques de stabilité

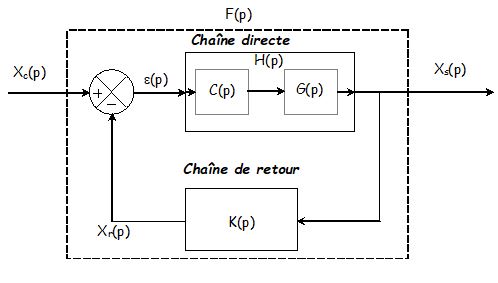
Ils permettent de prévoir la stabilité d’un système à partir de son étude en boucle ouverte ou fermée.

• \( F(p) = \frac{{H(p)}}{{1 + K(p)H(p)}} \) est la transmittance en Boucle Fermée. et
• \( T(p) = K(p)H(p) \) la transmittance en Boucle Ouverte.

Il s’agit donc de déterminer quand les zéros de \( 1 + T(p) \) (donc les pôles de F(p)) sont à partie réelle négative. La recherche de \( 1 + T(p) =0 \) amène plusieurs critères possible plus ou moins pratiques.

Critères de Bode

Diagramme de Bode

• en ordonnée \( G_{dB} \) en fonction de \( f \) et
• \( \varphi \) en fonction de \( f \)

A la vue du critère du revers, deux observations sont possibles

• Pour la pulsation \( \omega_c \) telle que \( \arg \left( {K(j{\omega _C})H(j{\omega _C})} \right) = - \pi \)
  • Si \( \left| {K(j{\omega _C})H(j{\omega _C})} \right| < 1 \) ou le gain \( {T_{dB}} = 20\log \left| {K(j{\omega _C})H(j{\omega _C})} \right| < 0 \): le système est stable
  • Si \( \left| {K(j{\omega _C})H(j{\omega _C})} \right| > 1 \) ou le gain \( {T_{dB}} = 20\log \left| {K(j{\omega _C})H(j{\omega _C})} \right| > 0 \): : le système est instable
• Pour la pulsation wu pour laquelle \( \left| {K(j{\omega _C})H(j{\omega _C})} \right| = 1 \) soit \( {T_{dB}} = 20\log \left| {K(j{\omega _C})H(j{\omega _C})} \right| = 0 \)
  • Si \( \varphi \left( {{\omega _u}} \right) > - \pi \) : système stable
  • Si \( \varphi \left( {{\omega _u}} \right) < - \pi \) : système instable

Critères de Nyquist

Plan de Nyquist

• en ordonnée : \( \Im(\underline{T}) \)
• en abscisses : \( \Re(\underline{T}) \).

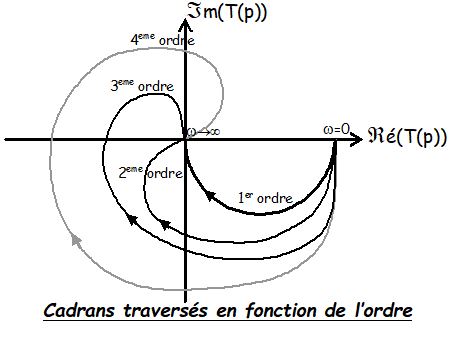
L’utilisation des critères algébriques est limitée aux systèmes sans retard. Lorsque p croît de \( -\infty \) à \( +\infty \) la transmittance en boucle ouverte \( T(p) = K(p)H(p) \) décrit une courbe.

Si elle exclut 0 par un demi cercle du coté des réels positif alors elle est fermée et appelée diagramme de Nyquist.

Ce qui se résout

• par le calcul en remplaçant \( p=j\omega \) et en traçant la FTBO
• expérimentalement en relevant pour chaque fréquence le module et l’argument de \( T(p) = K(p)H(p) \)

Attention : \( K(p)H(p) = C\frac{{N(p)}}{{D(p)}} = \frac{C}{{{{\underline{p}}^\alpha }}}\frac{{1 + {b_1} \underline{p} + ... + {b_m}{{\underline{p}}^m}}}{{1 + {a_1} \underline{p}+ ... + {a_n}{{\underline{p}}^n}}} \) et lorsque \( p \) tend vers 0 \( K(p)H(p) = \frac{C}{{{{\underline{p}}^\alpha }}} \) donc le passage de \( p=0^- \) à \( p=0^+ \) voit l’argument de \( K(p)H(p) \) passer de \( \alpha \frac{\pi }{2} \) à \( -\alpha \frac{\pi }{2} \) dans le sens horaire.

Pour éviter la détermination du passage de la courbe en p=0, on remplace parfois le critère de Nyquist par le critère du revers.

Critère du revers

Le système est stable en boucle fermée si le diagramme de Nyquist de la transmittance en BO \( K(p)H(p) \) laisse le point –1 sur sa gauche lorsque la pulsation \( \omega \) varie de \( 0^+ \) à l’infini. Le système est d’autant plus stable que l’on est loin de ce point.

Critères de Black

Plan de Black

• en ordonnée \( G_{dB} \)
• en abscisses : \( \varphi \) de la FTBO

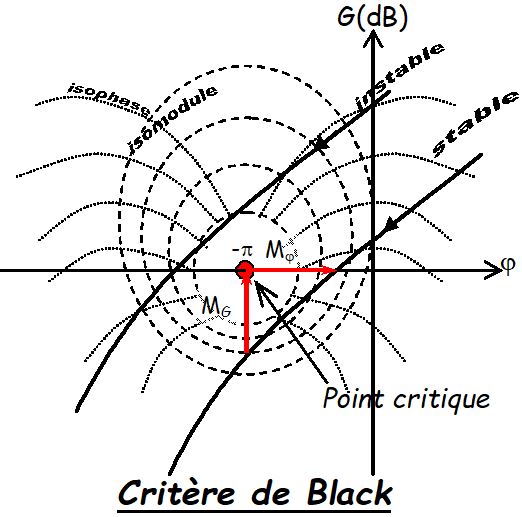
Le critère de stabilité est si on laisse le point critique à sa droite quand on décrit la courbe dans le sens des \( \omega \) croissants.