Transmittance d'un système:
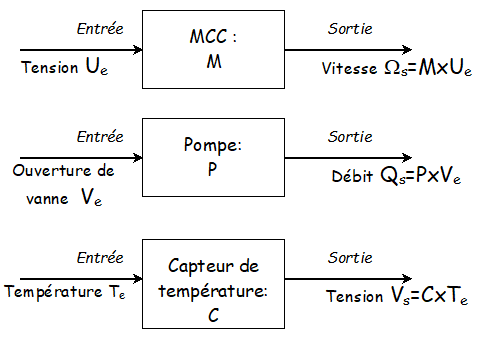
Exemples
Chaque système ou partie de système peut être représenté par un schéma bloc liant une grandeur d’entrée et une grandeur de sortie.
La transmittance est le coefficient (ou fonction) par lequel on multiplie l’entrée pour connaitre la sortie.
La transmittance est représentée par un bloc dont la grandeur entrante est multipliée par la valeur de la transmittance est la sortie est le résultat de cette multiplication
Sommateur/soustracteur:

Soustracteur
Afin d’affiner les dépendances entre entrées et sorties, une simple fonction linéaire n'est pas toujours suffisante, il est alors nécessaire d'ajouter l'addition et la soustraction à nos possibilités:
Chaque grandeur entrant dans le rond est comptabilisée positivement ou négativement en fonction du signe indiqué et la sortie est donc le résultat de cette addition/soustraction
Exemple d'un moteur à courant continu

En première approximation le schéma bloc d'un moteur à courant continu pourrait ressembler à çà:
Quelques transmittances plus complexes
Cette vision souvent suffisante est malgré tout limitée. Ces divers exemples ne tiennent pas compte par exemple du temps mis par le système pour atteindre son état stable. Des transmittances définies mathématiquement de façon plus fine sont parfois nécessaires.
Afin de tenir compte de la complexité des équations physiques des systèmes (à base d'équations différentielles liant nos entrées et nos sorties) il s'avèrera judicieux de transformer nos dérivées des équations différentielles par les variables de Laplace correspondantes.
La transformation de Laplace permettant ainsi de transformer nos équations différentielles en polynômes de \( p \).
- la dérivation donne : \( {\rm{L}}\left[ \frac{{de(t)}}{{dt}} \right] \mapsto p \times E(p) -e(0^+)\)
- l'intégration donne : \( {\rm{L}}\left[ \int {e(t)} \right] \mapsto \frac{{E(p)}}{p} \)
- le retard \( {\rm{L}}\left[ {e(t - T)} \right] \mapsto {e^{ - T \times p}} \cdot E(p) \)
Les transmittances du premier ordre
En prenant en compte l'inertie mécanique du moteur à courant continu le schéma bloc d'un moteur à courant continu pourrait ressembler à çà:

Les transmittances du second ordre
En prenant en compte l'inductance de l'induit du moteur à courant continu le schéma bloc d'un moteur à courant continu pourrait ressembler à çà:
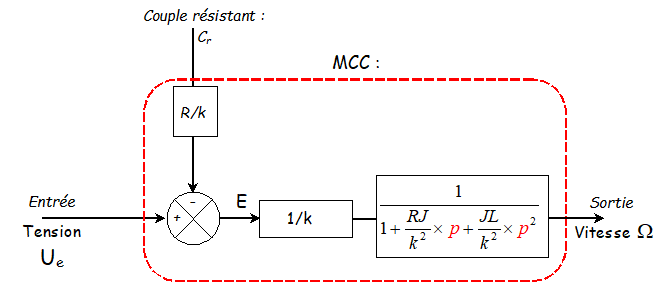
Comment déterminer la transmittance d'un système , capteur ou autre?
Deux cas se présentent :
- vous connaissez les lois physiques et relations de proportionnalités entre entrées et sorties, alors l'écriture de celles-ci doit permettre d'établir les transmittances.
- dans le cas contraire ou en guise de confirmation de l'étude précédente, un ou des essais expérimentaux vont permettre de mettre en évidence la proportionnalité entre entrée et sortie en régime stabilisé (gain statique), la vitesse de progression de la grandeur de sortie (constante de temps du système), et/ou la période des oscillations du systèmes (coefficient d'amortissement), et/ou le retard entre l'apparition de la consigne et le début de réaction de la sortie.
Un système donné par son équation différentielle dans l'espace temporel peut être de manière équivalente représenté dans le plan de Laplace par une équation algébrique. Ainsi, on convient de caractériser le système dans l'espace de Laplace par une fonction que l'on appelle la fonction de transfert du système. Cette fonction est définie comme le rapport entre la transformées de Laplace de la sortie sur la transformée de Laplace de l'entrée sous l'hypothèse que les conditions initiales sont toutes nulles (on s'intéresse seulement à l'étude de la réponse forcée du système).
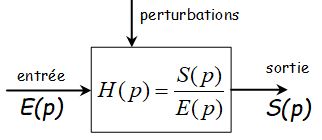
Opérations sur les fonctions de transfert
Blocs en série
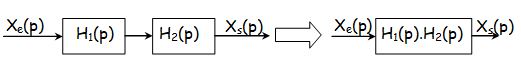
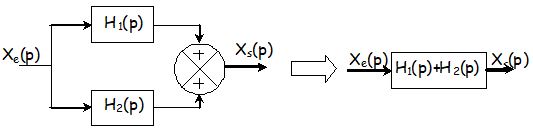
Blocs en parallèle
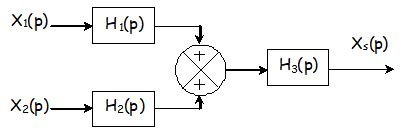
Blocs factorisés
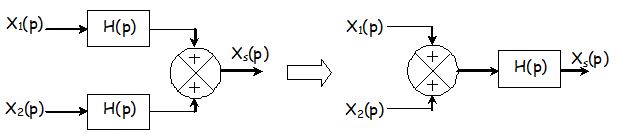
Principe de superposition
Pour calculer la fonction de transfert entre une entrée particulière et une sortie, on suppose ou on se placera dans une configuration annulant les autres entrées
Système à retour non unitaire
Ce schéma bloc est le maillon essentiel de toute régulation : on gagnera donc à connaitre son résultat par cœur
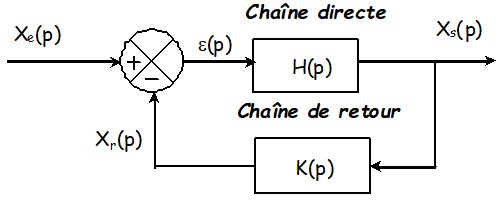
\( \frac{{{X_s}(p)}}{{{X_e}(p)}} = \frac{{H(p)}}{{1 + K(p)H(p)}} \)





