Théorème de Bernoulli sans perte ou gain d'énergie
Soit m une masse de fluide parfait (écoulement stationnaire isovolume, pas de frottement) entre les sections dS1 et dS2 à l'instant t (schéma ci-dessous); à l'instant t + dt, m se trouve entre dS1' et dS2'
Par application de la conservation de l’énergie, appliquée à cette masse m entre les instants t et t + dt , on montre que l'on peut écrire :
\( \rho \frac{{v_2^2}}{2} + \rho g{z_2} + {p_2} = \rho \frac{{v_1^2}}{2} + \rho g{z_1} + {p_1} = {C^{te}} \)
soit encore
| \( \rho \frac{{{v^2}}}{2} + \rho gz + p = C^{te} \) |
Ainsi sur une portion de conduite est fait un bilan énergétique
- du travail des forces de pression en W/m3, ou p la pression statique en Pa : p
- de l'énergie potentielle volumique en W/m3, ou la pression de pesanteur en Pa: \( \rho gz \)
- de l'énergie cinétique volumique en W/m3, ou la pression cinétique en Pa: \( \rho \frac{{v^2}}{2} \)
En divisant tous les termes de la relation précédente par le produit \( \rho g \), on écrit tous les termes dans la dimension d'une hauteur (pressions exprimées en mètres de colonne de fluide).
| \( \frac{{{v^2}}}{{2g}} + z + \frac{p}{{\rho g}} = H = {C^{te}} \) |
Avec cette fois-ci
- la hauteur de pression \(\frac{p}{\rho g} \)
- la hauteur dynamique \( \frac{{v^2}}{2g} \)
- la hauteur de position \( z \)
Lorsque, dans un écoulement d’un fluide parfait(sans pertes), il n'y a aucune machine (ni pompe ni turbine) entre les points (1) et (2) d'une même ligne de courant, la relation de Bernoulli peut s’écrire sous l'une ou l'autre des formes suivantes :
Forme mettant en jeu les énergies volumiques (dont la pression):
\( \frac{1}{2}\rho {\text{ }}\left( {v_2^2 - v_1^2} \right) + \rho g{\text{ }}({z_2} - {z_1}) + \left( {{p_2} - {p_1}} \right) = 0 \)
ou en divisant l'équation précédente par \( \rho \times g \), on fait apparaître la forme mettant en jeu les hauteurs manométriques :
\( \frac{1}{{2g}}{\text{ }}\left( {v_2^2 - v_1^2} \right) + ({z_2} - {z_1}) + \frac{{\left( {{p_2} - {p_1}} \right)}}{{\rho g}} = 0 \)
Théorème de Bernoulli avec perte ou gain d'énergie
Si les forces de frottements interviennent (Pf puissance dissipée < 0) ou lorsque le fluide traverse une machine hydraulique, il échange de l’énergie avec cette machine : la puissance P échangée est :
- P > 0 si l’énergie est reçue par le fluide (ex : pompe \( P_p \)) ;
- P < 0 si l’énergie est consommée par le fluide (ex : turbine \( P_t \) ou \( P_f \) frottements).
| \( \underbrace {\rho \frac{{v_1^2}}{2} + \rho g{z_1} + {p_1}}_{{\rm{énergies}}\,\,\,{\rm{volumiques}}\,\,{\rm{en}}\,\,{\rm{1}}} + \frac{{{P_f} + {P_T} + {P_P}}}{{{q_V}}}\, = \underbrace {\rho \frac{{v_2^2}}{2} + \rho g{z_2} + {p_2}}_{{\rm{énergies}}\,\,\,{\rm{volumiques}}\,\,{\rm{en}}\,\,{\rm{2}}} \) |
On pourra vérifier que de part et d'autre de cette équation les grandeurs sont des énergies volumiques en \( J/m^3 \)
Attach 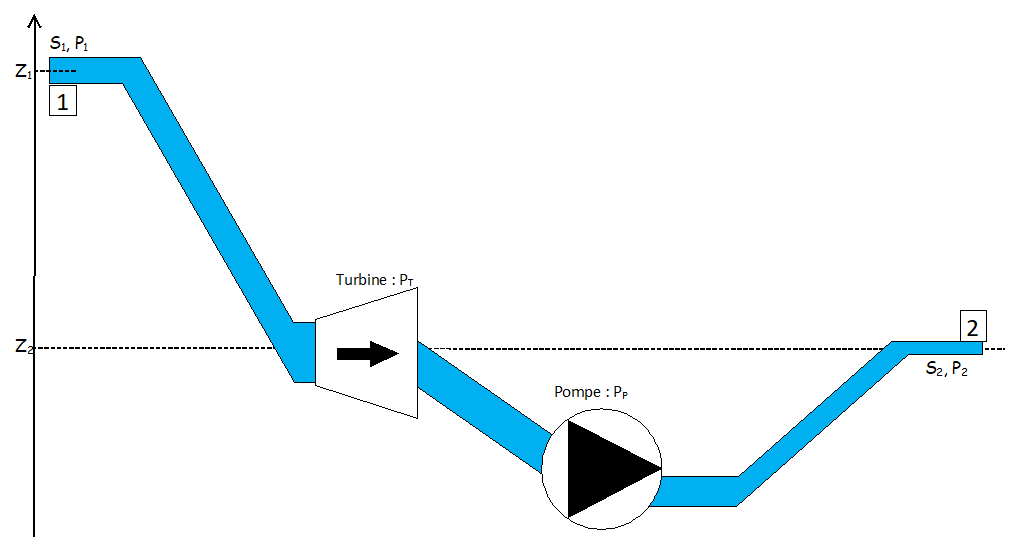
La caractéristique essentielle d'une pompe est sa capacité à amener de l'eau à une certaine hauteur et à lutter contre les frottements (autrement appelés pertes de charge):
- La pompe génère donc une hauteur nette ou hauteur manométrique:\( \Delta H = \frac{P}{{\rho g{Q_V}}} \) que l'on peut aussi lier au débit massique \(\Delta H = \frac{P}{{g{Q_m}}}\)
- La puissance de la pompe génère est donc proportionnelle à la surpression générée et au débit volumique \(P = {Q_V}\Delta p\)
Vidéos
La loi de Bernoulli (Christophe Finot) 9'38
| https://www.youtube.com/watch?v=P4NOWMsyE08 |
La physique animée : Théorème de Bernoulli, écoulement stationnaire d'un fluide parfait incompressible. 13'25"
| https://www.youtube.com/watch?v=E32YHDTDy-4 |
Une vidéo de 13 mn 24 qui permet de retrouver expérimentalement et analytiquement le théorème de Bernoulli et ses applications : Effet Venturi, formule de Torricelli, portance, tube de Pitot.
L'effet Venturi appliqué aux véhicules de course (ou effet de sol)






