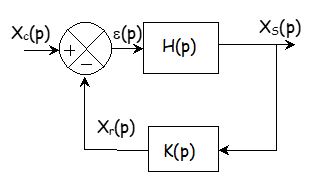
Un système est précis si la sortie suit l'entrée quelles que soient les circonstances.
L'écart ou erreur est la différence entre la valeur souhaitée et la valeur obtenue.
L’erreur est définie par \( \mathop {\lim }\limits_{t \to \infty } \varepsilon (t) \) soit en se servant du théorème de la valeur finale.
| \( \mathop {\lim }\limits_{t \to \infty } \varepsilon (t) = \mathop {\lim }\limits_{\underline{p} \to 0} \varepsilon (p) = \mathop {\lim }\limits_{\underline{p} \to 0} \frac{{{X_c}(p)}}{{1 + K(p)H(p)}} \) |
Et comme
\( K(p)H(p) = C\frac{{N(p)}}{{D(p)}} = \frac{C}{{{{\underline{p}}^\alpha }}}\frac{{1 + {b_1} \underline{p} + ... + {b_m}{{\underline{p}}^m}}}{{1 + {a_1} \underline{p}+ ... + {a_n}{{\underline{p}}^n}}} \)
et
\( \underline{\varepsilon} = \frac{{{{\underline{X}}_c}(p)}}{{1 + K(p)H(p)}} \)
il vient
\( \underline{\varepsilon}(p)\left[ {{{\underline{p}}^\alpha }\left( {1 + {a_1} \underline{p}+ ... + {a_n}{{\underline{p}}^n}} \right) + C\left( {1 + {b_1}\underline{p}+ ... + {b_m}{{\underline{p}}^m}} \right)} \right] = {\underline{X}_c}(p)\left[ {{{\underline{p}}^\alpha }\left( {1 + {a_1} \underline{p}+ ... + {a_n}{{\underline{p}}^n}} \right)} \right] \)
ce qui permet de relier les équations différentielles liant \( \epsilon \) et \( X_c \).
L’erreur est la valeur de \( \varepsilon \) en régime permanent.
Or \( K(p)H(p) = C\frac{{N(p)}}{{D(p)}} = \frac{C}{{{{\underline{p}}^\alpha }}}\frac{{1 + {b_1} \underline{p} + ... + {b_m}{{\underline{p}}^m}}}{{1 + {a_1} \underline{p}+ ... + {a_n}{{\underline{p}}^n}}} \) croit d’autant plus vite que \( \alpha \) et \( C \) sont grands (ainsi l’erreur tend vers 0 quand p tend vers 0) mais dans ce cas cela nuit à la stabilité du système (C augmente : diag de Nyquist enfle et si \( \alpha > 2 \) le diag de Nyquist tourne d’un angle sup à \( 2\pi \)).
Ceci nous confirme que précision et stabilité sont deux exigences contradictoires
On définit la classe des systèmes par la puissance \( \alpha \) soit le degré d’intégration du système.
- Pour les systèmes classiques leur classe est nulle : \( \alpha =0 \) (1er ordre, 2ème ordre, Strejc, Broïda)
- Le correcteur proportionnel intégral permet d’atteindre \( \alpha =1 \) ou plus en cas de mise en cascade.
| N.B. \( K(p)H(p) = C\frac{{N(p)}}{{D(p)}}\mathop \approx \limits_{p\, \to \,0} \frac{C}{{{p^\alpha }}} \) | FTBO de classe 0 : \( \alpha = 0 \) | FTBO de classe 1 : \( \alpha = 1 \) | FTBO de classe 2 : \( \alpha = 2 \) |
| Erreur de position
Entrée échelon : \( {x_c}(t) = E h(t) \) donc \( {\underline{X}_c}(p) = \frac{E}{p} \) | \( \mathop {\lim }\limits_{p \to 0} \frac{{p\frac{E}{p}}}{{1 + C}} = \frac{E}{{1 + C}} \)
l'erreur statique vaut \( \frac{E}{1+C} \) 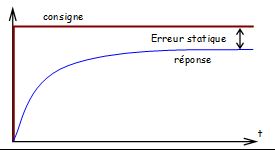 | \( \mathop {\lim }\limits_{p \to 0} \frac{{p \cdot \frac{E}{p}}}{{1 + \frac{C}{p}}} = 0 \)
l'erreur statique vaut 0 | l'erreur statique vaut 0 |
| Erreur de trainage
Entrée rampe: \( {x_c}(t) = E \cdot t h(t) \) donc \( {\underline{X}_c}(p) = \frac{E}{p^2} \) | \( \mathop {\lim }\limits_{p \to 0} \frac{{p\frac{E}{{{p^2}}}}}{{1 + C}} = \frac{E}{{p\left( {1 + C} \right)}} = + \infty \)
l'erreur de trainage augmente continuellement 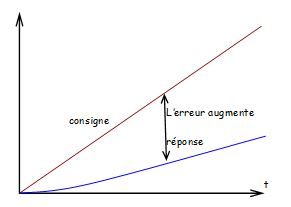 | \( \mathop {\lim }\limits_{p \to 0} \frac{{p\frac{E}{{{p^2}}}}}{{1 + \frac{C}{p}}} = \frac{E}{{p + C}} = \frac{E}{C} \)
l'erreur de trainage tend vers \( \frac{E}{C} \) 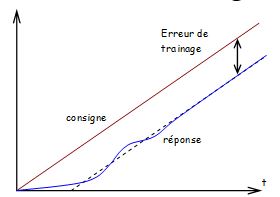 | \( \mathop {\lim }\limits_{p \to 0} \frac{{p\frac{E}{{{p^2}}}}}{{1 + \frac{C}{{{p^2}}}}} = \frac{E}{{p + \frac{C}{p}}} = 0 \)
l'erreur de trainage tend vers \( 0 \) 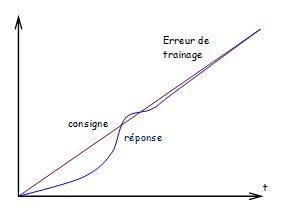 |
| Erreur d'accélération
Entrée parabole: \( {x_c}(t) = E \cdot t^2 h(t) \) donc \( {\underline{X}_c}(p) = \frac{2E}{p^3} \) | l'erreur d'accélération augmente continuellement
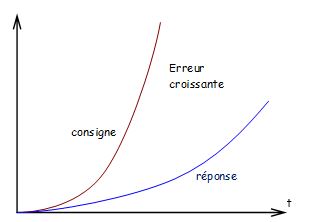 | \( \mathop {\lim }\limits_{p \to 0} \frac{{p\frac{{2E}}{{{p^3}}}}}{{1 + \frac{C}{p}}} = \frac{{2E}}{{{p^2} + \frac{C}{p}}} = + \infty \)
l'erreur d'accélération augmente continuellement 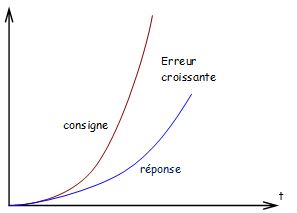 | \( \mathop {\lim }\limits_{p \to 0} \frac{{p\frac{{2E}}{{{p^3}}}}}{{1 + \frac{C}{{{p^2}}}}} = \frac{E}{{{p^2} + C}} = \frac{E}{C \) }
l'erreur d'accélération tend vers \( \frac{E}{C} \) 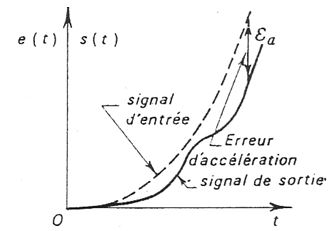 |





