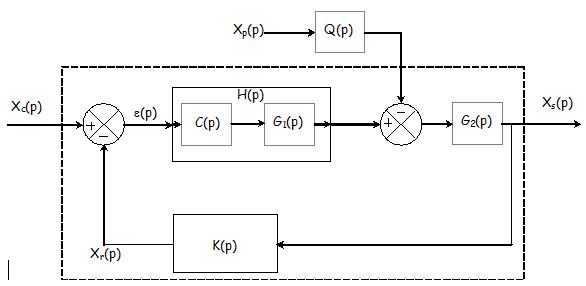
En écrivant les diverses relations :
\( {X_c} - {X_s}K = \varepsilon \)
\( \left( {\varepsilon H + {X_p}H} \right){G_2} = {X_s} \)
Et en les combinant il vient :
\( {X_c}\frac{H}{{\frac{1}{{G{}_2}} + KH}} + {X_p}\frac{Q}{{\frac{1}{{G{}_2}} + KH}} = {X_s} \)





