Un système est rapide si son temps de réponse est jugé satisfaisant.
- Le temps de réponse à 5%
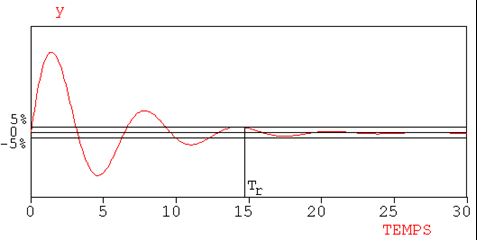
- \( t_{r5\%min} \) est le temps mis pour être compris entre 105 % et 95 % de la valeur finale.
- Remarque 1
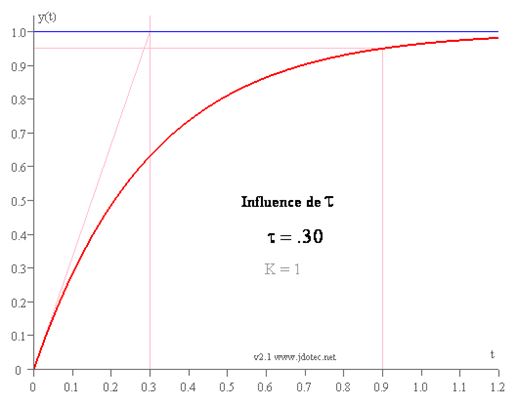
- Un système du premier ordre est caractérisé par un temps de réponse \( t_{r5\%min} = 3 \tau \)
- Remarque 2
- Dans le cas d’un système d’ordre 2, le système est caractérisé par son coefficient d’amortissement \( m \) qui s’il est trop important assurera un temps de réponse trop grand et s’il est trop faible des oscillations trop importantes.
On tolère d’un système un dépassement transitoire de 20 % : Pour un système d’ordre 2 (asservissement de position par exemple) \( d = \frac{{{X_{\max }} - {X_0}}}{{{X_0}}} = {e^{ - \pi \frac{m}{{\sqrt {1 - {m^2}} }}}} \) si \( d= 0,2 \) alors \( m = 0,45 \) ce qui se répercute par une remontée du régime harmonique de 2 dB
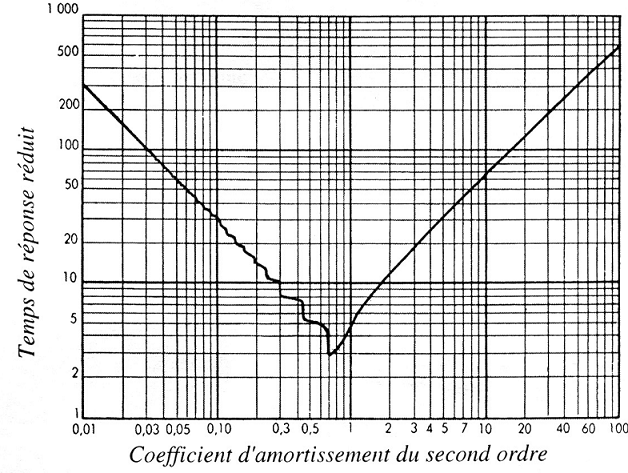
| L’abaque des temps de réponses : | L’abaque des dépassements |
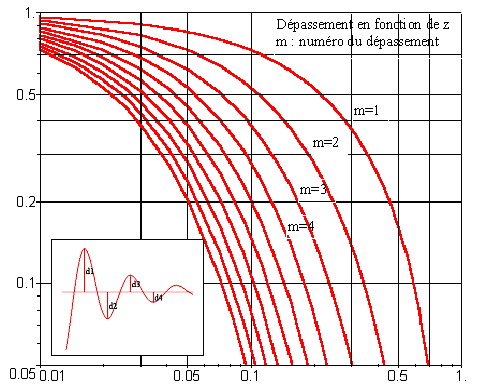
| permet de trouver le temps de réponse si l’on connaît \( m \) et \( \omega_n \) ou sur une courbe après avoir mesuré \( \omega_n \) et tr5% on peut en déduire m | (en pourcentage de la valeur finale) permet de déterminer le nombre et la valeur des dépassements
(en ordonnées : le pourcentage du dépassement et en abscisses : le coefficient d’amortissement) |
| 
|
| La partie gauche correspond à des régimes pseudo périodiques, La partie droite correspond à des régimes apériodiques En ordonnée le temps de réponse réduit est \( \omega_n \times T_{5\%} \) | La verticale passant par le m considéré croise les diverses courbes et donne ainsi le nombre et la valeur du dépassement en % |





