Transformateur dans l'hypothèse de Kapp

Simplifications

Dans l’hypothèse de Kapp ${N_1}{i_1} + {N_2}{i_2} = 0$ ∇ alors :

• $m = - \frac{\underline{I}_1}{\underline{I}_2}$ ∇

et

• $\frac{\underline{V}_{20}}{\underline{V}_1} = \frac{\underline{V}_{20}}{\underline{V'}_1 + \left( {{r_1} + j{\ell _{f1}}\omega } \right){\underline{I}_{10}}} \approx \frac{\underline{V}_{20}}{\underline{V'}_1} = - m$ ∇

L’approximation ainsi faite revient à considérer le schéma équivalent suivant:

∇

On remarque que l’on peut toujours introduire les pertes fer par la présence du courant Iµ courant absorbé à vide par le transformateur:

∇

On remarque que l’on peut toujours introduire les pertes fer par la présence du courant Iµ courant absorbé à vide par le transformateur. On considère donc que la chute de tension dan $r_1$ et $\ell_1$ est faible. On peut donc alimenter les pertes fer ($R_f$) et l'imperfection du circuit magnétique ($L_f$) par la tension $\underline V_1$.

∇

Schémas équivalents

Impédance ramenée au primaire : adaptation d’impédance

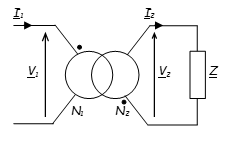
Si l’on considère un transformateur parfait ${\underline V_2} = - m \cdot {\underline V_1}$ et $- m \cdot {\underline I_2} = {\underline I_1}$ ∇

Or ${\underline V_2} = \underline Z \cdot {\underline I_2}$ donc ${\underline V_1} = \frac{ \underline Z }{m^2} \cdot {\underline I_1}$ .

Tout se passe comme si ${\underline Z'} = \frac{ \underline Z }{m^2}$ était branché directement aux bornes du primaire.

Le transformateur joue alors le rôle d’adaptateur d’impédance.

Schéma équivalent ramené au secondaire

Pour ramener les impédances $r_1$ et $\ell_{f1}$ au secondaire il suffit d’exprimer $U_2$ qu’en fonction des grandeurs du secondaire : $m = - \frac{\underline V'_2}{\underline V'_1} = \frac{\underline I_1}{\underline I_2}$ ${\underline V_2} = {\underline V_{20}} - \left[ {\underbrace {\left( {{m^2}{r_1} +{r_2}}\right)}_{{R_2}} + j\underbrace {\left( {{m^2}{\ell _{f1}} + {\ell _{f2}}} \right)}_{{L_2}}\omega } \right]{\underline I_2}$ Cela fait apparaître deux impédances : ${R_S} = {m^2}{r_1} + {r_2}$ et ${L_S} = {m^2}{\ell _{f1}} + {\ell _{f2}}$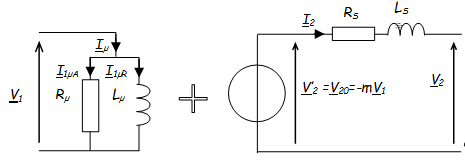

Schéma équivalent ramené au primaire

Pour ramener les impédances $r_2$ et $\ell_{f2}$ au primaire il suffit d’exprimer $V_1$ qu’en fonction des grandeurs du primaire : $m = - \frac{\underline V'_2}{\underline V'_1} = \frac{\underline I_1}{\underline I_2}$

En regroupant les termes ${\underline V_1} = - \frac{{{{\underline V}_2}}}{m} + \left[ {\underbrace {\left( {\frac{{{r_2}}}{{{m^2}}} + {r_1}} \right)}_{{R_1}} + j\underbrace {\left( {\frac{{{\ell _{f2}}}}{{{m^2}}} + {\ell _{f1}}} \right)}_{{L_1}}\omega } \right]{\underline I_1}$

Cela fait apparaître deux impédances : ${R_P} = \frac{{{r_2}}}{{{m^2}}} + {r_1}$ et ${L_P} = \frac{{{\ell _{f2}}}}{{{m^2}}} + {\ell _{f1}}$