Equations et schéma équivalent
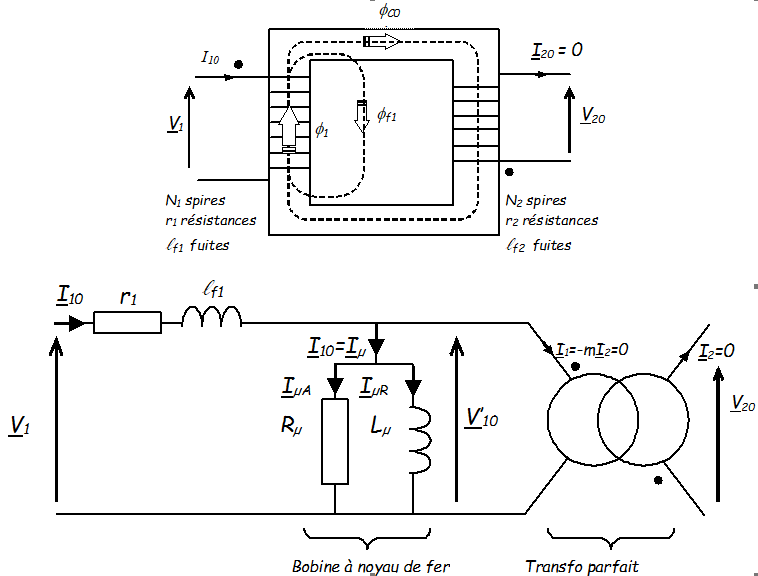
Le transformateur se comporte comme une bobine à noyau de fer :
Le fait qu'une partie du flux magnétique puisse s'échapper dans l'air donne l’équation des flux:
\( {\underline{\phi}_{10}} = {\underline{\phi}_{C0}} + {\underline{\phi}_{f1}} \)
d'où on tire l'équation de la tension du transformateur
\( {v_1} = {r_1}{i_{10}} + {N_1}\frac{{d{\phi _1}}}{{dt}} = {r_1}{i_{10}} + {N_1}\frac{{d\left( {{\phi _{f1}} + {\phi _{C0}}} \right)}}{{dt}} \)
\( {v_1} = {r_1}{i_{10}} + {N_1}\frac{{d\left( {\frac{{{N_1}{i_{10}}}}{{{\Re _{air}}}}} \right)}}{{dt}} + {N_1}\frac{{d{\phi _{C0}}}}{{dt}} \)
\( {v_1} = {r_1}{i_{10}} + \underbrace {{\ell _{f1}}}_{\frac{{N_1^2}}{{{\Re _{air}}}}}\frac{{d{i_{10}}}}{{dt}} + \underbrace {{N_1}\frac{{d{\phi _{C0}}}}{{dt}}}_{{{V'}_{10}}} \)
Si l’on considère le courant sinusoïdal ce qui n’est en toute rigueur pas le cas on peut passer aux grandeurs complexes.
\( {\underline{V}_1} = {r_1}{\underline{I}_{10}} + j{\ell _{f1}}\omega {\underline{I}_{10}} + j{N_1}\omega {\underline{\phi}_{C0}} \)
avec \( {\underline{V}'_{10}} = j{N_1}\omega {\underline{\phi}_{C0}} \) et \( {\underline{V}_2} = - j{N_2}\omega {\underline{\phi}_{C0}} \) ∇
- \( r_1 \) est la résistance interne de la bobine primaire
- \( \ell _{f1} \) est l’inductance de fuite primaire
- \( L_µ \) est l’inductance magnétisante
- \( R_F \) représente les pertes fer
Représentation de Fresnel

Bilan de puissances :
A vide le transformateur absorbe
- \( P_{10} = {r_1}I_{10}^2 + \frac{{V'}_{10}^2}{R_\mu } \,\,avec\, \left\{ \begin{array}{l} \\ {r_1} I_{10}^2 :pertes\,\,Joules\,\,de\,\,l'enroulement\,\,primaire\\ \frac{{V'}_{10}^2}{R_\mu }:pertes\,\,fer\,\,du\,\,circuit\,\,magnétique \end{array} \right. \) qui mesuré est égal à \( {P_{10}} = {V_1}{I_{10}}\cos {\varphi _{10}} \).
- \( Q_{10} = \ell_{f1} \omega I_{10}^2 + \frac{{V'}_{10}^2}{{L_\mu }\omega} \,\,avec\, \left\{ \begin{array}{l} {\ell _{f1}}\omega I_{10}^2 :puissance\,\,réactive\,\,de\,\,fuite\,\,dans\,\,l'enroulement\,\,primaire \\ \frac{{{V'}_{10}^2}}{{{L_\mu }\omega }} = {L_\mu }\omega I_{\mu R}^2:puissance\,\,magnétisante\,\,du\,\,circuit\,\,magnétique \\ \end{array} \right. \) qui mesuré est égal à .\( {Q_{10}} = {V_1}{I_{10}}\sin {\varphi _{10}} \)





