|
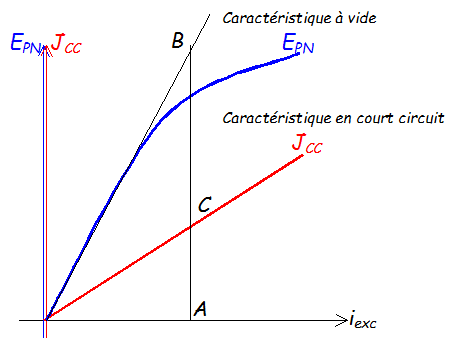
Etude à vide : détermination de \( E_{PN} \)
|
Le rotor et son champ sont entraînés par une turbine. Les bobines de l’induit sont alors le siège de f.é.m. alternative de pulsation \( \omega = p.\Omega_S \). Le courant débité par l'induit (le stator) étant nul, la tension entre phase et neutre est égale à la fém pour un enroulement soit \( E_{PN} = K p n N \phi_{max} \) En régime permanent, (fréquence de rotation n constante) \( E_{PN} \) ne dépend que de \( \phi_{max} \) , lui même fonction du courant d'excitation \( i_{exc} \).\( E_{PN} = K' \phi_{max}\) La caractéristique \( E_{PN} = f(i_{exc} ) \) est donc identique à celle de la courbe de magnétisation du circuit. 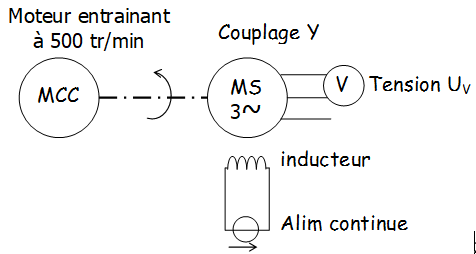 | 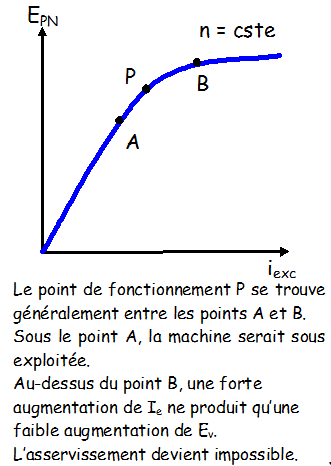
|
Etude en court-circuit
La caractéristique \( J_{cc} = f(i_{exc} \) à \( n = C^{ste} \) est une droite passant par l'origine ( il suffit donc d'une mesure pour la déterminer ). Elle permet la détermination de la réactance du modèle de l’alternateur.
 | 
|
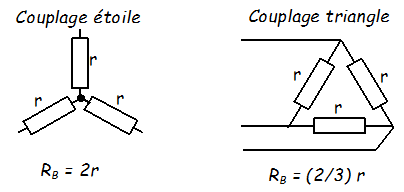
Détermination de r
Elle se fait par la mesure de la résistance \( R_B \) entre phases, par une méthode voltampèremétrique.
Détermination de X
On utilise l’essai en court-circuit de l'alternateur. En effet, \( Z = \frac{{{E_{PN}}({i_e})}}{{{J_{CC}}({i_e})}} \) (pour une valeur de \( i_{exc} \) fixée
ATTENTION : \( E_{PN} \) et \( J_{cc} \) doivent être obtenus pour une même valeur de courant d'excitation \( i_{exc} \) .
la détermination proposée suppose le circuit magnétique non saturé. Elle reste néanmoins valable pour des circuits peu saturés : pour cela, on linéarise la caractéristique à vide. Si la machine est saturée, l'impédance synchrone n'est plus constante, et sa valeur doit être déterminée pour chaque point de fonctionnement.
Alors
| \( X =\sqrt{Z^2 - r^2} \) |