Modèle de Machine Synchrone

Modèle équivalent de Behn Eschenburg pour un enroulement d’alternateur

Modèle retenu

Le modèle équivalent de Behn Eschenburg ne prend pas en compte la saturation du matériau a contrario du diagramme de Potier

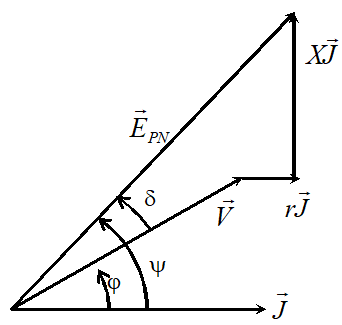
\( {{\underline E}_{PN}} = r \underline J + jX \underline J+ \underline V \)

\( V (V)\) est la tension aux bornes d’un enroulement de la machine \( E_{PN} (V)\) est la fém à vide ou fém synchrone : elle ne dépend que de \( i_{eN} \) si n est fixée. \( r (\Omega) \) est la résistance de l'enroulement : très souvent négligée. \( X (\Omega) \) traduit la chute de tension due à la réaction magnétique d'induit: elle est appelée réactance synchrone. \( \varphi \) est imposé par la charge qu'alimente l'alternateur

Remarque le déphasage entre \( e_{PN} \) et v est appelé angle décalage interne. On le note \( \delta \) Il peut être déterminé expérimentalement.

Établissement du modèle de Behn-Eschenburg

On considère un fonctionnement en alternateur.

A vide, la tension par phase est \( E_V \). En charge, la tension par phase sera \( V \), entre deux phases : \( U \).

Le courant est orienté en convention générateur.

Le modèle équivalent suppose des grandeurs linéaires (en particulier un circuit magnétique non saturé et une machine à pôles lisses).

Le flux total \( \phi _T \) est la somme du flux résultant \( \phi _R \) (créant la tension induite) et du flux de fuite \( \phi _f \) donc \( \phi _T = \phi _R + \phi _f\).

• La résistance r d’une phase de l’alternateur crée une chute de tension \( rJ \) que l’on négligera souvent car très inférieure aux autres chutes de tension.
• Le flux de fuite \( \phi _f \) est modélisé par une inductance \( \lambda \) et ainsi \( \phi _f = \lambda I\)
• La réaction magnétique d’induit : en charge, les enroulements d'induit (du stator) sont parcourus par un système triphasé de courants. Ils créent donc un champ magnétique tournant qui se superpose au champ magnétique inducteur. C'est la réaction magnétique d'induit. Cette réaction magnétique d'induit dépend de \( J \) , mais aussi de \( \varphi \) déphasage imposé par la charge. On peut modéliser \( \phi (J) \) par une réactance traduisant la réaction magnétique d’induit (RMI) \( \phi (J) = LJ\) .
• Le flux résultant \( \phi _R \) reçu par l’induit est la somme du flux inducteur \( \phi (i_{exc}) \) et du flux du au courant de l’induit \( \phi (J) \) donc :\( \underline \phi _R = \underline \phi (i_{exc}) + \underline \phi (J) \)

Comme \( \underline \phi _R = \underline \phi (i_{exc}) + \underline \phi (J) \) Donc \( \underline \phi _T = \underline \phi _R+ \underline \phi _f = \underline \phi (i_{exc}) + L \underline J + \lambda \underline J\).

Comme \( \underline E = - \frac{d \underline \phi}{dt} = - j\omega \underline \phi\) (loi de Faraday)

\( {\underline E_R} = \underline E({i_{exc}}) - jL\omega \underline J \) : tension induite résultante de l’action du champ inducteur et de la RMI

\( \underline V = {\underline E_R} - r \underline J- j\lambda \omega \underline J \): tension fournie par l’alternateur donc tension induite moins les pertes

\( V = E({i_{exc}}) - jL\omega J - rJ - j\lambda \omega \)

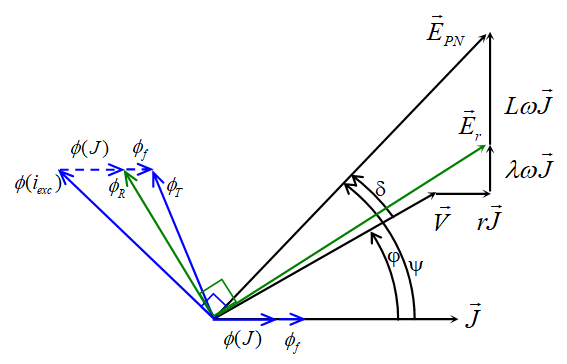
\( V = E({i_{exc}}) - rJ - j\underbrace {\left( {\lambda + L} \right)\omega }_XJ \)

Avec \( X = \left( {\lambda + L} \right)\omega \) la réactance synchrone

L’angle \( \varphi \) est imposé par la charge \( \underline \phi (i_{exc}) \) est perpendiculaire à \( \vec E_{PN} \) \( \underline \phi _T \) est perpendiculaire à \( \vec E_{r} \)

Diagramme de Potier (prise en compte de la saturation du matériau):

On considère un fonctionnement en alternateur : A vide, la tension par phase est EV. En charge, la tension par phase sera V, entre deux phases : U. Le modèle équivalent suppose des grandeurs linéaires (en particulier un circuit magnétique saturé et une machine à pôles lisses) ; le courant est orienté en convention générateur.