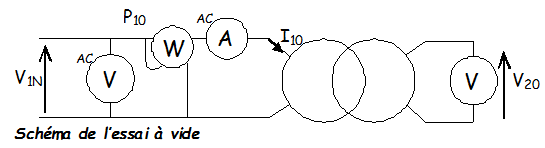
L'essai à vide va permettre de déterminer :
- le rapport de transformation
| \( m \approx \frac{{{V_{20}}}}{{{V_1}}} \) |
- la résistance modélisant les pertes fer \( R_f \): \( {P_{fer}} = {P_{10}} - \underbrace {{P_{j10}}}_{{r_1}I_{10}^2} \) et donc \( R_f \) car \( {P_{fer}}\mathop \approx \limits_{Kapp} \frac{{V_1^2}}{{{R_f }}} \)
| \( {R_f}\mathop \approx \limits_{Kapp} \frac{{V_1^2}}{{{P_{fer} }}} \) |
- l'inductance magnétisante traduisant le caractère imparfait du matériau ferromagnétique \( L_µ \)
\( Q_{10} = \sqrt {S_{10}^2 - P_{10}^2} = \sqrt {{{\left( {{V_1}{I_{10}}} \right)}^2} - P_{10}^2} = \ell _{f1} \omega \times I_{10}^2 + \frac{V\prime _1^2}{L_\mu \omega } \mathop \approx \limits_{Kapp} \frac{V_1^2}{L_\mu \omega } \mathop \approx \limits_{Kapp} Q_{10} \)
| \( L_\mu \approx \frac{V_1^2}{Q_{10} \omega} \) |