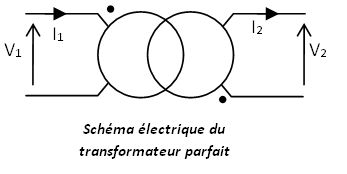
Relation fondamentale sur les tensions

Si on fait rentrer un courant par les bornes homologues, il apparaît une fém e telle que la bobine se comporte comme un générateur.
Toutes les pertes sont négligées : le flux traverse donc les deux bobinages. Ainsi :
\( v_1 = -e_1 = N_1 \frac{d \phi}{dt} \) et \( v_2 = -e_2 = N_2 \frac{d \phi}{dt} \) ∇
Comme la variation de flux est commune aux deux bobines on en déduit:
donc
| \( \Rightarrow \frac{\underline V_2}{\underline V_1} = -\frac{N_2}{N_1}\) |
∇
donc \( \underline V_2= - m \underline V_1\) ∇
Le signe - traduit l'opposition de phase entre le primaire et le secondaire
Rapport de transformation
Le rapport de transformation m est défini par :
| \( m = \frac{V_{20}}{V_{1N}} = \frac{N_2}{N_1}\) |
avec
- \( V_{20} \) tension efficace au secondaire à vide
- \( V_{1N} \) tension efficace au primaire
- \( N_1 \) et \( N_2 \) nombres de spires au primaire et au secondaire.
Relation de Boucherot :
La relation de Boucherot lie la tension induite dans une bobine soumise à un champ magnétique sinusoïdal d'une fréquence donnée.
Si on suppose que le champ varie de façon sinusoïdale alors \( b(t)= \hat{B} sin \omega t \).
Donc comme \( v_1 \) est \( N_1 \) fois la dérivée du flux traversant la bobine : \( v_1 = N_1 \frac{d(S \hat B sin \omega t)}{dt} = N_1 \omega S \hat B cos \omega t\).
L'amplitude de \( v_1(t) \) est \( N_1 2 \pi f S \hat B \) et est aussi égale à \( V_1 \sqrt{2}\) donc
| \( V_1 = 4,44 N_1 f S \hat B \) |
| \( V_2 = 4,44 N_2 f S \hat B \) |
avec
- f: la fréquence du champ magnétique en Hz
- \( \hat B \): la valeur maximale du champ magnétique en Tesla
- S: la section du circuit magnétique en m²
Relation sur les courants :
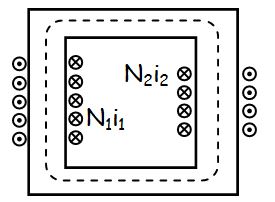
Si on applique le théorème de Gauss sur le contour parcouru par le flux \( \phi_C \) alors :
\( N_1 i_1 + N_2 i_2 = \Re \varphi \)
Si on considère la perméabilité du matériau \( \mu \) très grande donc \( \Re \approx 0\)
On en déduit que \( N_1 i_1 + N_2 i_2 = 0 \) donc \( \frac{N_2}{N_1} = - \frac{i_1}{i_2} \) donc \( \underline i_1 =- m \underline i_2 \) ∇
On a donc avec les conventions choisies
| \( m = \frac{V_{20}}{V_{1N}} = \frac{N_2}{N_1}=\frac{I_{1N}}{I_{2N}}\) |
Le bilan des puissances:
Le bilan des puissances est simple : la charge au niveau du secondaire impose le déphasage \( \varphi \) entre les tensions et courants du secondaire et par conséquent entre la tension et le courant du primaire.
Comme le transformateur est parfait, il n'y a pas de pertes de puissances active ou réactive dans le transformateur.
\( P_1 = V_1.I_1.cos\varphi_1 = P_2 = V_2.I_2.cos \varphi_2 \)
et \( \varphi_1 = \varphi_2 \)
\( Q_1 = Q_2 = V_2.I_2.sin \varphi_2 = V_1.I_1.sin \varphi_1\)
\( S_1 = V_1.I_1= V_2.I_2= S_2. \)





