Equations et schéma équivalent
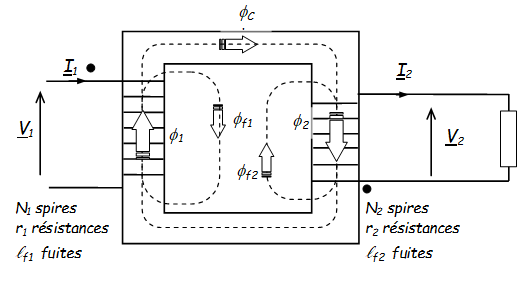
| Primaire | Secondaire | |
| Flux | \( {\underline{\phi}_{1}} = {\underline{\phi}_{f1}} + {\underline{\phi}_{C}} \) | \( {\underline{\phi}_{2}} = {\underline{\phi}_{f2}} + {\underline{\phi}_{C}} \) |
| Tensions | En convention récepteur \( {v_1} = {r_1}{i_1} + {N_1}\frac{{d{\phi _1}}}{{dt}} \) \( {v_1} = {r_1}{i_1} + {N_1}\frac{{d{\phi _{f1}}}}{{dt}} + {N_1}\frac{{d{\phi _C}}}{{dt}} \) | En convention générateur \( {v_2} = -{r_2}{i_2} - {N_2}\frac{{d{\phi _2}}}{{dt}} \) ∇ \( {v_2} = -{r_2}{i_2} - {N_2}\frac{{d{\phi _{f2}}}}{{dt}} + {N_2}\frac{{d{\phi _C}}}{{dt}} \) ∇ |
| Gauss | \({\phi _{f1}} = \frac{{{N_1}{i_1}}}{{{\Re _{air}}}}\) et \({\phi _C} = \frac{{{N_1}{i_1}}}{{{\Re _{fer}}}}\) | \({\phi _{f2}} = \frac{{{N_2}{i_2}}}{{{\Re _{air}}}}\) et \({\phi _C} = \frac{{{N_2}{i_2}}}{{{\Re _{fer}}}}\) ∇ |
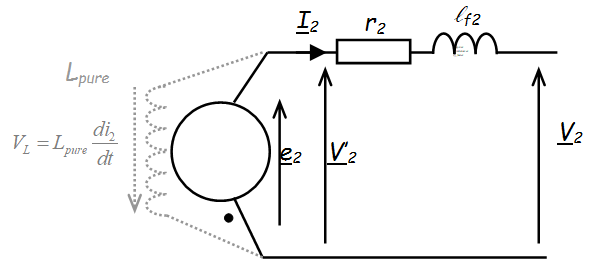
| Tensions | \({v_1} = {r_1}{i_1} + {\ell _{f1}}\frac{{d{i_1}}}{{dt}} + \underbrace {{N_1}\frac{{d{\phi _C}}}{{dt}}}_{{{V'}_1}}\) avec \( {V'_1} = {N_1}\frac{{d{\phi _C}}}{{dt}} = \underbrace {\frac{{N_1^2}}{{{\Re _{fer}}}}}_{{L_{pure}}}\frac{{d{i_1}}}{{dt}} \) ∇ | \({v_2} = - {r_2}{i_2} - {\ell _{f2}}\frac{{d{i_2}}}{{dt}}\underbrace { - {N_2}\frac{{d{\phi _C}}}{{dt}}}_{{{V'}_2}}\) avec \({V'_2} = - {N_2}\frac{{d{\phi _C}}}{{dt}} = - \underbrace {\frac{{N_2^2}}{{{\Re _{fer}}}}}_{{L_{pure}}}\frac{{d{i_2}}}{{dt}}\) ∇ |
| Schémas | 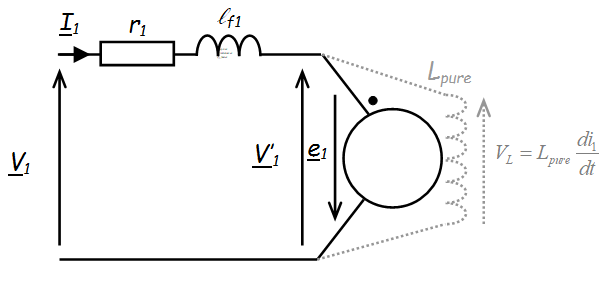
| 
|
On s’aperçoit alors que le rapport de transformation
\( m = - \frac{{{{\underline{V'}}_2}}}{{{{\underline{V'}}_1}}} = \frac{{{N_2}}}{{{N_1}}} \) ∇
Un bilan plus précis des ampères tours donne:
\( {N_1}{i_1} + {N_2}{i_2} = \Re \varphi \) ∇
Si l’on ne néglige pas la force magnétomotrice \( \Re \varphi \) alors on peut identifier cette perte d’ampère tours à un courant magnétisant que l’on trouve d’ailleurs à vide (le courant secondaire étant nul) : \( {N_1}{i_1} + {N_2}{i_2} = {N_1}{i_\mu } \) ∇ soit en complexe \( {N_1}{\underline{I}_1} + {N_2}{\underline{I}_2} = {N_1}{\underline{I}_\mu } \) ∇donc
\( {\underline{I}_1} = - m{\underline{I}_2} + {\underline{I}_\mu } \)∇
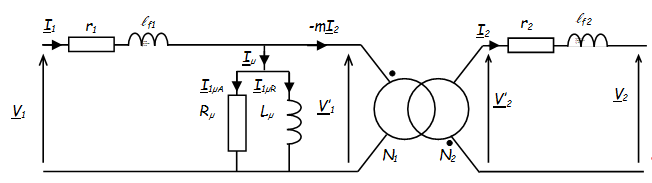
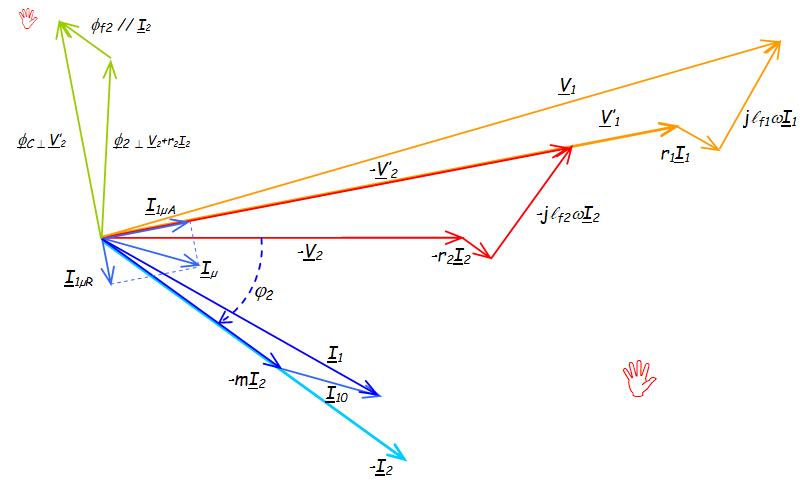
Représentation de Fresnel
- On prend \( V_2 \) comme origine des phases
- l'angle entre \( V_2 \) et \( I_2 \) est imposé par la charge
- la tension \( r_2 I_2\) est parallèle à \( I_2 \)
- la tension\( j \ell_{f2} \omega I_2\) est perpendiculaire à \( I_2 \)
- la somme des trois tensions précédentes donne \( V'_2 \)
- le rapport de transformation donne \( V'_1 = V'_2 / m \)
- de la même manière on trace le courant au primaire \( mI_2 \)
- La tension \( V'_1 \) est aux bornes
- de la résistance modélisant les pertes fer parcourue par un courant \( I_{1µA} \) en phase avec \( V'_1 \)
- de l'inductance magnétisante traduisant l'imperfection du circuit magnétique par un courant \( I_{1µR} \) perpendiculaire à \( V'_1 \)
- la somme des deux courants donne \( I_{1µ} \) qui s'ajoute à \( mI_2 \) pour donner \( I_1 \)
- la tension \( r_1 I_1\) est parallèle à \( I_1 \)
- la tension\( j \ell_{f1} \omega I_1\) est perpendiculaire à \( I_1 \)
- la somme des deux tensions précédentes et de \( V'_1 \) donne \( V'_2 \)
Le transformateur en charge (4'53") https://youtu.be/4_3EDEDQFOo
Vidéo réalisée sur la base d'une application de l'UJF de Grenoble (M. Oddon)
0:00 1:00 Chute de tension 1:30 triangle de Kapp 1:40 tension de court circuit compromis chute de tension/courant de court circuit 3:00 pertes fer et cuivre 3:50 cout d'un transfo (à vide VS en charge) 4:27 Pointe de courant à la mise sous tension
Bilan des puissances






