
|
On considère une machine non saturée. E=cte OB décrit une circonférence de centre O et de rayon E.
Si V, f et ie (donc E) sont constants, Pmax correspond à \( \delta=\pi/2 \). Si le couple résistant est supérieur à \( T_{max}= \frac{P_{max}}{\Omega_S} \) , le moteur décroche. (\( \Omega_S=2\pi n_S=2\pi.f/p \)). Pour P donné, AH est constant. Le point de fonctionnement B se déplace sur une droite parallèle à V dite droite d’équipuissance. |
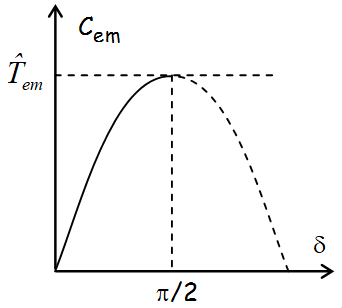
| D’après cette expression du couple \( {C_e} = \frac{{3V{E_V}\sin \delta }}{{L\omega \Omega }} \)
Il apparaît que le maximum de puissance est atteint pour \( \delta=\pi/2 \) |

| Sur wiki BTS |
1, place De Lattre de Tassigny
Vétraz-Monthoux BP241
74106 ANNEMASSE Cedex
mail
Téléphone : +33 (0)4.50.87.18.36
- Autopilotage de la machine synchrone
- Bilan de puissances
- Bilan sur la machine synchrone
- Caractéristique a tension constante courant d'excitation variable
- Caractéristique en charge courant d'excitation variable
- Caractéristique en court circuit
- Caractéristique à vide
- Caractéristiques en charge variable
- Comparaisons des moteurs AC et DC
- Compensateur synchrone
- Constitution
- Couplage sur le réseau
- Courbes de Mordey
- Détermination expérimentale du modèle équivalent
- Excitation de la MS
- Expression du couple moteur
- Fonctionnement moteur à excitation constante
- Force électromotrice induite
- Modèle de Machine Synchrone
- Moteurs Brushless
- Plaque signalétique
- Principe de la Machine Synchrone
- Relations du modèle équivalent simplifié
- Réaction Magnétique de l'Induit
- Réversibilité de la machine synchrone
- Schéma équivalent
- Symbole de la machine synchrone




