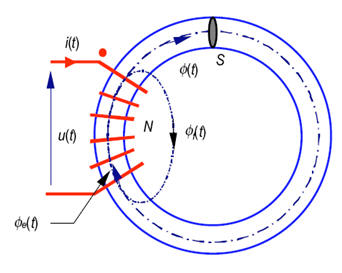
Toutes les lignes de champ créées par l’enroulement ne bouclent pas dans le circuit magnétique. Pour des raisons essentiellement de fabrication, certaines d’entre-elles se rebouclent dans l’air proche des spires.
On distingue:
- le flux dans le matériau \( \varphi (t) \)
- du flux de fuite s’en échappant \( \varphi_f (t) \)
- ainsi le flux embrassé par l’enroulement s’écrit : \( {\varphi _e}(t) = \varphi (t) + {\varphi _f}(t) \)
Donc par la loi de Faraday la tension est \( u(t) = N\frac{{d{\varphi _e}(t)}}{{dt}} = N\frac{{d\varphi (t)}}{{dt}} + N\frac{{d{\varphi _f}(t)}}{{dt}} \)
Et comme la loi d’Hopkinson nous donne \( Ni = \Re \cdot \varphi \) si on pose \( L = \frac{{{N^2}}}{\Re } \) alors : \( u(t) = L\frac{{di(t)}}{{dt}} + {\ell _f}\frac{{di(t)}}{{dt}} \)
avec \( {\ell _f} = \frac{{{N^2}}}{{{\Re _{air}}}} \) mais pour laquelle \( {\Re _{air}} \) n’est pas physiquement défini car il ne correspond pas à un parcours précis
Et comme \( \varphi = \frac{{Ni}}{\Re } = \frac{L}{N}i \) alors \( \phi = N\varphi = Li \)
On peut rajouter le caractère résistif du fil ainsi les 3 paramètres suivants caractérisent la bobine :
- Résistance : \( r = \rho \frac{\ell }{s} \)
- Coefficient d’auto induction : \( L = \frac{{{N^2}}}{\Re } \)
- Inductances de fuites : \( {\ell _f} \)
Ainsi \( u(t) = L\frac{{di(t)}}{{dt}} + {\ell _f}\frac{{di(t)}}{{dt}} + r \cdot i(t) \)
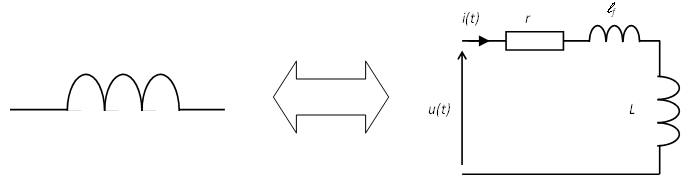
Remarque : pour réduire les fuites les enroulements sont placés au plus près du circuit magnétique. Les dispositions pratiques consistent à utiliser des circuits magnétiques cuirassés ou toriques :






