Force de Lorentz et Laplace
Un champ magnétique exerce sur les charges électriques en mouvement des forces qui sont responsables des mouvements observés.
Dans le cas des particules chargées : loi de Lorentz
|
La force de Lorentz, appliquée à la particule est le produit vectoriel
| 
|
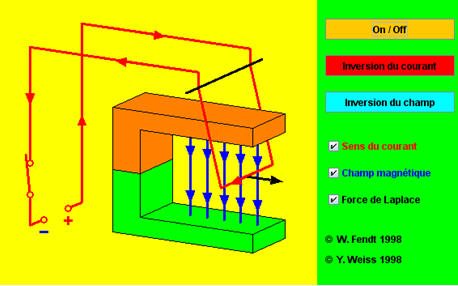
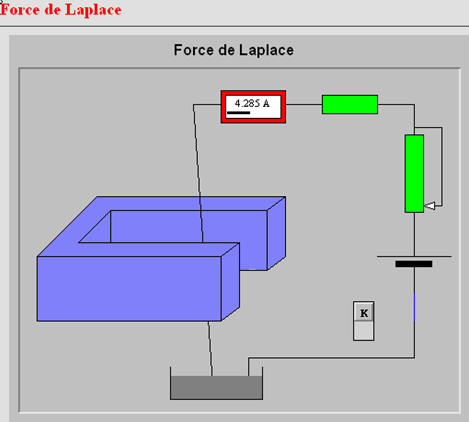
Dans le cas d’un conducteur parcouru par un courant I: loi de Laplace
Les charges se déplacent dans le conducteur tel que \( q = i \cdot t \) et \( \vec v = \frac{{\vec \ell }}{t} \) donc \( \vec F = q\vec v \wedge \vec B = q\frac{{\vec \ell }}{t} \wedge \vec B = i\vec \ell \wedge \vec B \) On définit le vecteur \( \vec \ell \) : vecteur orienté dans le sens de I et de norme égale à la longueur de fil plongé dans le champ \( \vec B \) La force exercée par le champ magnétique sur le conducteur est appelée force de Laplace:
| \(\vec F = i\vec \ell \wedge \vec B \) |
Le travail des forces de Laplace :
\( dW = d\vec F \cdot d\vec x = \left[ {id\vec \ell \wedge \vec B} \right] \cdot d\vec x = i\left[ {d\vec x \wedge d\vec \ell } \right] \cdot \vec B = i\vec B \cdot \vec ndS = i.d\Phi \)
La variation d’énergie occasionnée par le déplacement d’un élément de circuit est égale au produit du courant par le flux coupé.
Animation
Vidéo
| Vidéo de Anais Bearzi (0'48") Force de Lorentz 0'23" |
| https://youtu.be/s-WkVhm8C3Y |
| rayonnement cathodique (1'12") Patrick Poirier |
| https://youtu.be/FckJZfja1Ec |