Modélisation
A cause de la saturation du matériau ferromagnétique le courant n'est pas sinusoïdal.
La puissance transmise à la bobine est en partie perdue en pertes fer.
Les pertes fer dépendent de la tension d'alimentation (mais aussi de la fréquence de la tension d'alimentation).
La mesure de la puissance active avec un wattmètre fournit la somme des pertes fer (pour une fréquence fixée): \( P_{fer} \) .
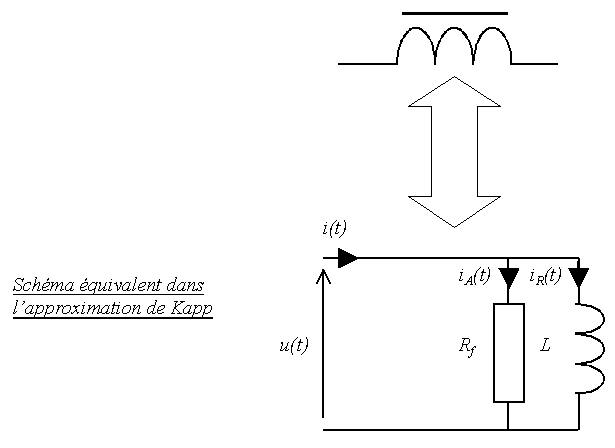
On peut modéliser ces pertes par une résistance \( R_f \) soumise à la tension u(t).
- Dans le cadre de l’approximation de Kapp (qui néglige les fuites et la résistance du fil : \( {\ell _f}\frac{{di(t)}}{{dt}}\,\,{\text{et}}\,r\,i(t)\,\, \ll {\text{à }}\,\,N\frac{{d\phi (t)}}{{dt}} \)), la puissance active absorbée par la bobine correspond aux pertes fer, la puissance réactive correspond à l'inductance. On en déduit donc :
- la résistance \( R_f \) modélisant les pertes fer \( {R_f} = \frac{{{U^2}}}{{{P_{fer}}}} = \frac{{{P_{fer}}}}{{I_A^2}} = \frac{U}{{{I_A}}} \)
- la réactance magnétisante, et donc l'inductance : \( X = L\omega = \frac{{{U^2}}}{{{Q_{fer}}}} = \frac{{{Q_{fer}}}}{{I_R^2}} = \frac{U}{{{I_R}}} \)
On notera tout de même que ces paramètres ne traduisent qu’une approximation car Rf et L ne sont pas constant et dépendent de la saturation du matériau et de la fréquence d’utilisation
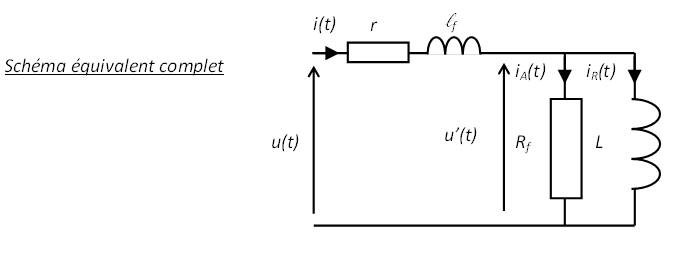
Pour tenir compte des paramètres \( \ell_f \) et \( r \) il suffit de les rajouter.
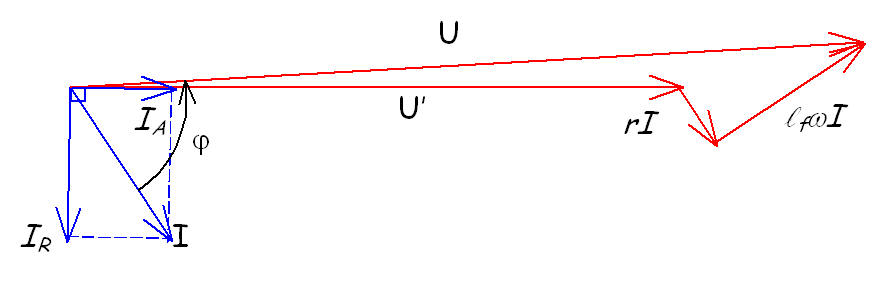
Représentation de Fresnel:
La représentation de Fresnel des divers courants et tensions est la suivante