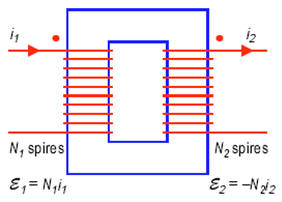
L'analyse d'un circuit magnétique dans le cadre de l’approximation linéaire d’Hopkinson implique les circuits magnétiques parfaits, c’est à dire linéaires (μr constant) et exempts de fuites magnétiques (tout le flux créé par les enroulements apparaît dans le circuit magnétique).
Dans le circuit magnétique, \( \vec B \) est uniforme, constante sur une section droite du circuit magnétique et le long de la ligne de champ moyenne (\( \ell \)).
Pour rappel le flux est tel que \( \varphi = B \cdot S. \)
Le théorème d’Ampère (sur la ligne moyenne) permet de déterminer l'excitation magnétique créée par les spires de courants \( NI \) : \( H \cdot \ell = NI = \mathcal{E} \)
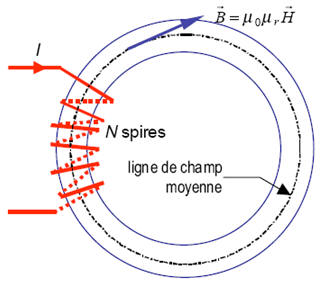
On détermine alors l'expression de \( H \) alors : \( H = \frac{B}{\mu } = \frac{B}{{{\mu _0}{\mu _r}}} = \frac{1}{{{\mu _0}{\mu _r}}} \cdot \frac{\varphi }{S} \)
d’où la relation \( \mathcal{E}= H \cdot \ell = \frac{1}{{{\mu _0}{\mu _r}}} \cdot \frac{\varphi }{S}\ell \)
Il apparaît donc une relation linéaire entre la force magnétomotrice \( \mathcal{E} \) (fmm) et le flux \( \varphi \).
Ceux-ci étant liés par les paramètres physique du matériaux :\( \mu , \ell et S \). On regroupe donc les paramètres physiques sous un seul terme que l'on appellera de reluctance
| \( \Re = \frac{\ell }{{\mu S}} \) |
La reluctance joue dans un circuit magnétique, vis à vis du flux magnétique, le même rôle qu'une résistance dans un circuit électrique vis à vis du courant électrique.
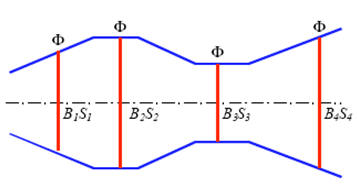
Comme on a émis l'hypothèse d'un circuit sans fuites de flux , on considère donc que le flux est conservatif. Ceci permettra de déterminer le champ B en chaque point du circuit magnétique.
Si plusieurs bobinages coexistent, il faut sommer les influences des fmm. Les contributions de chaque bobinages s'ajoutent s'ils s'enroulent dans le même sens autour du circuit magnétique.
\( \mathcal{E} = \sum\limits_k {{\alpha _k}{N_k}{i_k}} \)
Le coefficient \( \alpha _k \) traduit le sens de la fmm. Il est obtenu en appliquant la règle des points homologues : Des courants entrants par les points homologues de différents bobinages placés sur un circuit magnétique créent des forces magnétomotrices qui s’ajoutent
On écrit donc la relation d’Hopkinson :
| \( \sum\limits_k {{\alpha _k}{N_k}{i_k}} = \left( {\sum\limits_i {{\Re _i}} } \right) \cdot \varphi \) |