Wiki du BTS Electrotechnique - SA - Fonction exponentielle d'un premier oprdre

Contents [hide]

Rappels sur la fonction exponentielle et ses valeurs particulières

Rappels sur la fonction exponentielle

$e^{-\infty}=0$ et $e^0=1$ .
l'inverse de la fonction exponentielle : $e^x$ est la fonction logarithme népérien $ln(x)$ , $ln(e^x)=x=e^{ln x}$ .
un petit détour vers cette merveilleuse fonction logarithme permettra d'en dévoiler quelques secrets.

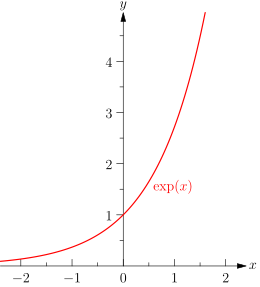
Etudions les valeurs particulières de cette fonction de façon à pouvoir retrouver sur un oscillogramme la valeur de la constante de temps.

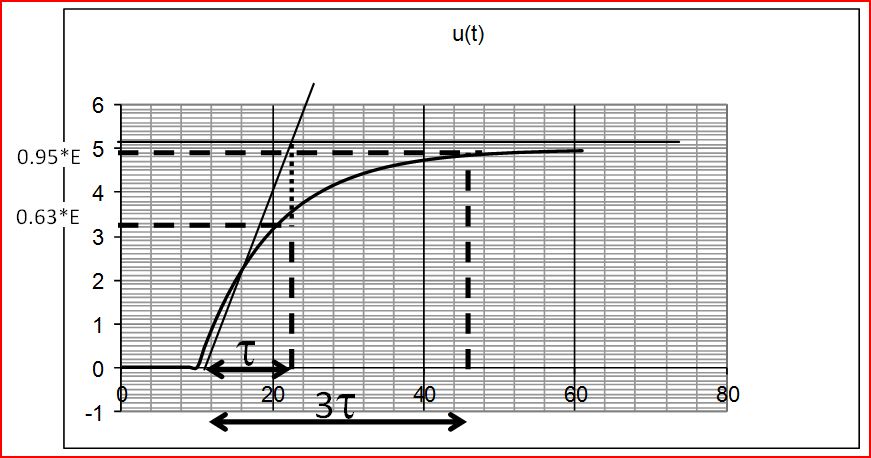
Calculons la valeur de $(1 - {e^{ - t/\tau }})$ pour $\tau$ et $3\tau$

$t=\tau$	$e^{ - t/\tau }=0.37$ soit 37 %	$(1-e^{ - t/\tau })=0.63$ soit 63 %
$t=3\tau$	$e^{ - t/\tau }=0.05$ soit 5 %	$(1-e^{ - t/\tau })=0.95$ soit 95 %

Donc pour trouver la valeur de $\tau$ il suffit de trouver sur le signal étudié la valeur telle que y(t) soit égale à 63% de sa valeur max et de regarder à quel temps correspond cette valeur pour en déduire $\tau$ ( 37% du max pour une décroissance) On définit le temps de réponse : $t_{r5\%}$ : le temps au bout duquel la tension u ne diffère que de 5% de sa valeur finale donc $t_{r5\%}=3 \times \tau$
Une autre méthode consiste à tracer la tangente à l’origine de la courbe ainsi que la droite asymptotique, l’écart temporel entre leur intersection et l’origine de la courbe est égal à $\tau$
On définit parfois le temps de montée tm comme le temps de passage de 10% à 90% de la valeur max soit $2,2 \tau$